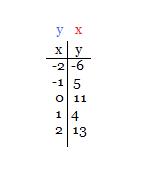Scribe Post: Day 15

Hi guys! This is Jann(again) and I'll be your scribe for today. (^_^)

Today we talked about Identities.

Fundamental Identities:

tangent= sine/cosine

cosecant= 1/sine

secant= 1/cosine

cotangent= cosine/sine

Pythagorean Identities:

sin^2 + cos^2= 1

1 + cot^2= csc^2

tan^2 + 1= sec^2

Sum & Difference Identities:

sin(a+/-B) = sin a cos B +/- cos a sinB

cos(a+/-B) = cos a cos B -/+ sin a sin B

Note: Mr. K showed us how to do the "Sine Dance". It will help us remember the formula. The actions are like this:

Double Angle Identities:

sin2= (2sin)(cos)
cos2= (cos^2)-(2sin^2)

cos2= 2cos^2 - 1

Then after that, we were given these questions.

1. Sketch the graph of

If you look at the properties, you should have something like this:

The properties are:

- shifts the graph up by 1.

- reflects the graph towards the x-axis.

- shifts the graph to the right by 1.

Note: The formula of the period is:

Note: The standard form for a sine function is f(x)= AsinB(x-C)+D; where A=amplitude, B= Period, C= face shift, D= vertical shift.

2. Write 2 equations, 1 sine and 1 cosine for this graph.

The class came up with these 2 formulas:

f(x)= 3cos2x-1

A= 3

B= 2

C= 0
D= -1

f(x)= 3sin2 [x-("pi"/4)]-1

A= 3

B= 2

C= "pi"/4

D=-1

Lastly, we plotted this table in our calculator.

Note: This information is real! Its based on the real average temperatures in Winnipeg.

Here are the steps to graph this table:

i) Make sure your lists are clear. Press [2nd] then [+]. Press [4] for "ClrAllLists".

ii) Press [Stat] then [1].

iii) Enter the numbers on the table. Month in L1 and Temperature on L2.(Note: Plug in no. "1" for Jan, "2" for Feb, etc.)

iv) Press [2nd] then [Y=]. Make sure your plots are on and on the right list number.

v) Press [Zoom] then [9]. Hit [Enter].

To calculate the reg,

-Press [Stat] the arrow right to "Calc"

-Arrow down till you see "SinReg".

-Enter L1, L2, Y1. Hit [Enter].

You should see something like this:

y=a*sin(bx+c)+d

a=19.49038889

b= .4657581446
c= -1.720934653

d= .5227365909

I think thats all we did today. Whew....(-_-)

Finally, if there's something wrong, please with the capital P, post a comment.(^_^)

Oh, and the next scribe is Charlotte! (cuz your the last one on the first cycle)

scribe post day 14

today in class all we did was review for stuff that we learned in grade 12. there were questions on the board as usual. He went throught the two projects that we are supposed to do for this course. he also talked about how we should start to make our groups. he also stated that the video project is supposed to no more than 10 minutes and one minute is too short.

here are some of the questions that Mr.K put on the board. we didn't get to go through all of them since we didn't have enough time.

1) suppose f(X)=x₂-1 find:

A) (f o g)(X)
B) (g o f)(X)
C) h(X) = ((f o g) o (g 0 f)) (X)


A) sin₂ = (sinx-1)(sinx+1)
-all we have to do to this question is plug g(X) into f(X)
-you can also use the difference of squares


B) sin(X₂ -1)
= sin((X+1)(X-1)) ...you could this but it would make it more complicating
****NEVER DO THIS****----> sinX₂... sin is not a number its a function

C) sin₂ (sin(X₂ -1)) - 1


2) find the exact value:
A) sin(pi/3) X cos(5pi/6) + tan(-3pi/4)




this all we go up to.. sry guys.. i don't wanna post answers up on this if i know its not for sure right.

Just like Mr.K said in class ""REMEMBER PATTERNS INSTEAD OF FACTS, PATTERNS CONTAIN A WEALTH OF FACTS"


The unit circle contains many patterns. With these patterns you will memorize the unit circle easier.


REMEMBER "" 1, 2, 3 ""

When using this pattern you always start from the origin. you don't have to mind the denominator because it is always 2, all you have to really care about it the numerator. count ""1, 2, 3 "" from the origin. Count right to find the "COS" value and up to find the ""SIN" value. As you can see from the picture its pretty simple but very hard to explain. So i think that will not explain it because i will just end up confussing you guys.

Well i guess this is practically all we have learned in this class. Mr.K talked about alot of other patterns but they don't apply to us so i won't even mention it.

NO HOMEWORK!!!
PRE-TEST IS ON FRIDAY AND TEST ON MONDAY
don't forget to post up you BOBS before the test.

OH YEAH and the next scribe is MARK!!!!

Scribe Post: Day 13

HI everyone! It's Katrin and I will be your scriber for today! :) Sorry for posting this super late!!! I took a nap after work and ended up waking up late!!! =)

Today, Mr. K started talking about Calculus AB and Calculus BC. He said that Calculus AB (the course we're all taking right now) has about nine chapters in the textbook that we're going to take up. Calculus BC is some other math course. Then, he started talking about the "Complete Solution Guide," a book that consists of answers from the text. He said that we can look at it at a regular basis for reference. He placed that on top of the filing cabinet by the window. He then started talking about the TEST!!!

The test consists of 3 parts:

1) blogging on blogging (BOB) <-- 1 mark (i think)
--Have you blogged before this test? will be asked...

2) multiple choice

3) long answers


***Test is going to be by the end of the week!!! Friday, I think!!!! *** NOT ANYMORE!!! Mr. K changed it to Monday!!!***


Mr. K continued and said that the post on the blog will have a series of questions.

IMPORTANT!

Mr. K also noted that the blogging on blogging (short, BOB) MUST BE LABELED when writing a post!!! Label post ---> BOB

and

Make the post before the test!!! (preferably days before the test and do sooner than later!)


We then did our daily questions....

1) If a ploynomial function , f, of degree of 3 has the numbers -6, 4 and 5 as zeros. If f(1)=210, determine the formula for f.

I started off by making the equation f(x) = (x+6) (x-4) (x-5)

----> remember to put opposite signs for -6, 4 and 5 b/c they're zeros!

Mr. K then taught me to make k as the "constant" and plug it in front of the zeros in order to have f(1)=210.

like this,

f(x) = k (x+6) (x-4) (x-5)
210= k (1+6) (1-4) (1-5)
210= k (7) (-3) (-4)
210 = 84k
84....... 84
2.5=k

therefore, we apply f(1)=210 in the equation...

f(x) = k (x+6) (x-4) (x-5)
f(1) = 2.5 (x+6) (x-4) (x-5)
f(1)= 2.5 (1+6) (1-4) (1-5)
f(1)= 2.5 (7) (-3) (-4)
f(1) = 210


2) A rational function g has the line x=2 and x=-2 as vertical asymptotes, the line y=4 as a horizontal asymptote and the numbers 1 and 3 as zeros. Find a formula for g.

clue used 1st: roots --> 1 and 3

g(x)=(x-1)(x-3)

---> goes in the numerator (above line)


clue used 2nd: vertical asymptotes x=2 and x=-2

g(x)=(x-1)(x-3)
..........(x-2)(x+2) <----(x² -4)

---> goes in the denominator (below line)


clue used 3rd: horizontal asymptote y=4

g(x)=4(x-1)(x-3)
..........(x-2)(x+2)

---> you have to look at the degree of the numerator and the degree of the
denominator...

---> if the degree of the numerator is smaller than the degree of the denominator
and if the degrees are the same in both the numerator and the denominator,
then there is a horizontal asymptote...
but...
if the degree of the numerator is greater than the degree of the denominator,
then there is NO horizontal asymptote...

---> highest power of x in numerator and divide by highest power of x in denominator...

..............the result of doing the arrowed (--->) steps is horizontal asymptote=1
BUT...
..............we don't want the horizontal asympote to equal 1, we want it to equal 4 since in the question it said that y=4 for the horiontal asymptote.

therefore, we put 4 as constant... like such:

g(x)=4(x-1)(x-3) which can be written as g(x)=x²-4x+3
........(x-2)(x+2)..................................................x²-4


3) Let f(x) = ax+b,
.....................cx-a
where a, b and c are positive contants. Show that f is one-to-one and f is its own inverse.

f(f^-1(x))=x

therefore you plug in f(x) in the equation itself... like such:

f(f(x))=a (ax+b) + b
_______(cx-a)____
_____c (ax+b) - a
______(cx-a)
f(f(x))=a(ax+b) + b(cx-a)
......... ____cx-a_______
_____c(ax+b) - a(cx-a)
.......................cx-a
f(f(x))=a(ax+b) + b(cx-a) x ____ cx-a______
....................cx-a__________c(ax+b) - a(cx-a)
f(f(x))=a(ax+b) + b(cx-a)
..............(cx+b) - a(cx-a)
f(f(x))=ax² + ab + bcx - ab
.............acx + cb - acx + a²
f(f(x))=a²x + bcx
...............cb+a²
f(f(x))=x(a² + bc)
.............a² + cb
f(f(x))=x

therefore when the final answer is equal to x, then it proves that f is one-to-one and f is its own inverse.


After thoose three questions Mr. K talked about Composition of Functions

f(x)=x - 1.........................g(x)=x - 2
......x + 4.................................. x

domain of f cannot = -4
domain of g cannot = 0

we have to plug in the function g(x) into f(x) so wherever you see x in f(x) you plug in the function of g(x)... like such...

f(x)=x - 1........................g(x)=x - 2
.........x + 4.................................x

f(g(x))=(x-2) - 1
....... _ (x)______
..............(x-2) + 4
................(x)
f(g(x))=(x-2) - (x)
............__x__ x___
..............(x-2) + 4x
.................x.......x
f(g(x))=-2__
..............5x-2 , x cannot = 2/5 and 0


Exclude:

5x-2=0
5x=2
x=2/5

and

x-2 = -4
x
x-2 = -4x
5x-2=0


Well... i don't really get composition of functions so i'm don' t really know how to explain this
much....

Homework: 1.9 odd #'s and study for quiz!!!

This is my scribe =) and I'm very very sorry for posting this super late!!! Well, i hope i covered everything we did in class today! hmmm... if i did anything wrong please feel free to comment since i'm not 100% sure about everything i posted... and oh yeah... the next scribe for tommorow will be CHARLENE!!! hehe i know u know already... but i know i still have to post it anyway! ;)

You're probably wondering why this scribe post is up soo late..well I'm really sorry but I had work and don't get home till 10:30 so it's really impossible for me to make the 9:00pm deadline.

Well today in math class we had a substitute, Ms. Nato or Ms.N. Mr. K was gone the whole day, probably at home eating turkey? haha just kidding. Anyway today's assignment is in the calculus textbook.
Read section 1.8 pg 51-57
Complete odd problems pg 58-61

Umm.. I think that's it? Wow what a short scribe post. Well I don't know about you guys but I'm hungry, tired and sleepy so bye for now.

Oh I know Katrin already knows she's scribe for tomorrow but I'm going to make it official, so tomorrows scribe is Katrin =).

Lessons from the Geese?

The geese who inhabit the wildlife preserve where we walk each day have hunkered down away from humans, preparing I think for their migration. Occasional small formations of geese fly to and from the preserve these days, but they don’t come looking for food from us as they did in spring. I wonder if you see them, too, heading south for the winter flying along in "V" formation? Do you know what science has discovered as to why they fly that way?

FACT 1 - As each Goose flaps its wings it creates uplift for the birds that follow. By flying in a V formation, the whole flock adds 71 per cent greater flying range than if each bird flew alone.

FACT 2 - When a Goose falls out of formation, it suddenly feels the drag and resistance of flying alone. It quickly moves back into formation to take advantage of the lifting power of the bird immediately in front of it.

FACT 3 - When the lead Goose tires, it rotates back into the formation and another Goose flies to the point position.

FACT 4 - The Geese flying in formation honk to encourage those up front to keep up their speed.

FACT 5 - When a Goose gets sick, wounded or shot down, two Geese drop out of formation and follow it down to help and protect it. They stay with it until it dies or is able to fly again. Then, they launch out with another formation or catch up with the flock.

Are there lessons we can learn from a gaggle of geese? What do you think?

Christian's comment, with Lindsay's "me too" really captured much of what many see as lessons from the geese. I wonder if Christian doesn't really have something when he says: "Beyond pointing out the mistakes, why don't we teach each other strategies on 'how to beat calculus'? That would work so great. May I suggest we try striving to work like these geese?" Here are how many others see the lessons from the geese and Christian's suggestions are a central theme.

FACT 1 - As each Goose flaps its wings it creates uplift for the birds that follow. By flying in a V formation, the whole flock adds 71 per cent greater flying range than if each bird flew alone.

LESSON - People who share a common direction and sense of community can get where they are going more quickly and easily because they are traveling on the thrust of one another.

FACT 2 - When a Goose falls out of formation, it suddenly feels the drag and resistance of flying alone. It quickly moves back into formation to take advantage of the lifting power of the bird immediately in front of it.

LESSON - If we are as smart as a Goose we stay in formation with those headed where we want to go. We are willing to accept their help and give our help to others.

FACT 3 - When the lead Goose tires, it rotates back into the formation and another Goose flies to the point position.

LESSON - It pays to take turns doing the hard tasks and sharing leadership. As with Geese, people are interdependent on each other's skills, capabilities and unique arrangements of gifts, talents or resources.

FACT 4 - The Geese flying in formation honk to encourage those up front to keep up their speed.

LESSON - We need to make sure our honking is encouraging. In groups where there is encouragement, the production is much greater. The power of encouragement (to stand by one's heart or core values and encourage the heart and core of other) is the quality of honking we seek.

FACT 5 - When a Goose gets sick, wounded or shot down, two Geese drop out of formation and follow it down to help and protect it. They stay with it until it dies or is able to fly again. Then, they launch out with another formation or catch up with the flock.

LESSON - If we have the wisdom of Geese, we will stand by each other in difficult times as well as when we are strong.

I wonder if "Learn Hard" and "Remember the Geese" together will help secure your road to excellence?

Scribe Post: Day 11

Good day to you all, I'm Christian, your scribe. Sorry I wasn't able
to post this right away. There were very important matters I had to
attend to AND I forgot how to put posts up. Thanks MARK for
reminding me how. Thanks to LINDSAY and CHARLOTTE too for teaching me how to put exponents and subscripts here. I'll go on with our lesson shortly.

INTRODUCTION TO LOGARITHMS '06

Over the week we learned about functions, inverse functions. It is
easy most of the time to solve for variables because we only need
to use simple operations. For example, when solving for x in the
equation (x + 5) / 2 = 6, we:

Step 1: Multiply both sides by 2
x + 5 = 12

Step 2: Subtract 5 from both sides
x = 7

In this case we only used multiplication and subtraction to solve for x. What happens if the variable we're looking for is an exponent? We can use our basic operations as well, but first we must understand what logarithms are, and when we should use them. Logarithms are exponents. When we are solving for an exponent in an equation, we are essentially solving the logarithm for that exponent. Look at the general equation for logarithms:

Log_ba = c

For this one, b represents the base, a represents the power, and c the exponent. Notice that there is an equal sign between the log expression and c. What does that mean? LOGS ARE EXPONENTS! If logarithms are exponents, to work with a log, we must understand this: In theory, since logs are exponents, the rules of logs and exponents must be the same right? Yes. The rules of logarithms describe what's happening to the exponents. Hence we must understand the rules of exponents.

RULES OF EXPONENTS

We learned these rules in grade 12 pre-calculus. This will just be a quick review. As a note again, and to make things clear here, I followed up the "cases" with the general equation in logarithms. As I mentioned, the rules of logarithms describe what happens to the exponents. We simply apply the exponent rules, and from there we can already manipulate our logs.

Case 1: When we multiply terms with the same base, we add the exponents.

(b^x)(b^y) = b^x+y

Let's apply this to some value:

This rule states that:
(3⁴)(3⁵) = 3⁴⁺⁵
= 3⁹

In logs, this means that:
logx + logy = log(xy)


Case 2: When we divide terms with the same base, we subtract the exponents.

(b^x) / (b^y) = b^x-y

Again, applying to specific values, this rule states that:

(3⁵) / (3⁴) = 3^5-4
= 3¹

In logs, this means that:

log(x/y) = logx - logy



Case 3: When we have a base raised to an exponent and the whole term is raised to another exponent, we multiply the exponents.

(b^x)y = b⁽x)(y)
= b^xy

The rule states that:

(3^4)⁵ = 3⁽⁴⁾⁽⁵⁾
= 3²⁰

In logs, this means that:

log_b(x)^y = (log_bx)(log_by)

= ylog_b(x)

Case 4: The Change of Base Law. This law states that if we have a log written in any base, we can switch the bases. We can easily solve logs of base "10" and base "e", because these are programmed in our calculator.

Take out your calculator. Turn it on. Clear the screen. If we press the log button, log( will come out right? What we do next is we enter the power, close the bracket, enter, and we get our value. What do you notice in terms of the structure of a log? We did NOT enter the base! What happens then if we are given bases of 2, 900, or 3.2562435234? We apply the Change of Base Law.

This law states that:

log_ba = log(a) / log(b)

For example:

log₃4 = log(4) / log (3)

YAY! Then we had bus ridership, and that was our class. Sorry again for posting late. Please visit this.

The next scribe is Anh.

Feel free to add and comment to this. Be nice, though, I have a very fragile ego.

logarithms assignment, group 3

Group 3: Suzanne, Christian, Mark

 
 
 
 
#3)ln(A/B)=lnA+ln(1/B)
We found out that this equation is true, here is our solution...
One of the laws of logarithms is: log(M/N)=logM-logN, also known as the Quotient law .
Using the Quotient law, ln(A/B)=lnA+ln(1/B), the blue part can be simplified to ln(A/B)=lnA+ln1-lnB.
 
 
 
ln(A/B)=lnA+ln1-lnB           
 
          
  
 
 
If you solve for ln1, it equals 0. So our equation, ln(A/B)=lnA+ln1-lnB
simplifies to ln(A/B)=lnA+0-lnB              
 
 
 
ln(A/B)=lnA-lnB                  The equation holds true, if you go back to our Quotient law (log(M/N)=logM-logN). 
 
 
 
ln(A/B)=lnA-lnB can be simplifed to  ln(A/B)=ln(A/B)
or
ln(A/B)=lnA-lnB can be simplified to lnA-lnB=LnA-ln B
 
 
 
 

Here is a possible mistake a person might make when writing this equation as: 
 
 
 
ln(A/B)=lnA-ln(1/B)
 
 
 
Instead of using the quotient law correctly, someone may subtract ln(1/B).  IF they subtract  like this, they have made their first mistake.>>>ln(A/B)=lnA-(ln1-lnB) 
 
 
 
ln(A/B)=lnA-(0+lnB)
 
 
 
The right side of the equation results in an addition, WHICH IS DIFFERENT FROM THE QUOTIENT LAW.  ln(A/B)=lnA+lnB
The above equation would simplify to this:
ln(A/B)=ln(AB) SEE THE DIFFERENCE?on the left side the values are being divided.  On the right side, the values are multiplied
 
 
 
The reason  someone might do this is by mistakenly applying the logarithmic law log(M/N)=logM-logN to this question twice.

Manny, Linger and Charlene

Our group consisted of Manny, Linger and myself. We were given question number one to do which is...



We had to prove if this equation is true or false.

Our group decided that this equation is TRUE


To Prove This:






Common Mistake:

A common mistake would be to use the power to power law


Which would obviously make the equation false


So yeah this what our group came up with. If anyone thinks its wrong or has comments just leave a comment :)

Group (4) - Jann, Jessica (loso) and Katrin

QUESTION # 4

(4) Show and explain why the following equation is TRUE or FALSE.

e ^{-ln c} = -c

Our group believes this equation is FALSE...

because


as an example, when we sub in the number "2" in for "c"

e ^{-ln c} = -c

e ^-ln(2) = -(2)
0.5 = -2


As you can see... both sides of the equation don't equal each other...


Therefore the equation is FALSE...


In order to make the equation become TRUE, our group came up with two methods.


METHOD 1:

ORIGINAL EQUATION: e^{-ln c} = -c

We changed "-c" to " 1/c " (both negative reciprocals of each other) and we sub in the number "2" in for "c" in order to make both sides equal.

e ^{-ln c} = 1/c
e ^{-ln (2)} = 1/(2)
0.5=0.5 =] they equal


METHOD 2:

ORIGINAL EQUATION: e ^{-ln c} = -c

In this case, we took the negative (-) out of both "ln c" and "c" and we sub in the number "2" in for "c" in order to make both sides equal.

e ^{ln c} = c
e ^{ln (2)} = (2)
2=2 =] they equal

So yeah... that's what our group came up with! If anyone has any comments regarding any mistakes we've made, feel free to comment! ; )

Group 5: Crystal, Danny, Lindsay

Group 5 --> Crystal, Danny, Lindsay

5) Prove how the following equation is TRUE or FALSE.

[log_b(x)]^y = ylog_b(x)

We believe that this is false.

If this was to be true, it would have to be:

log_b(x)^y = ylog_b(x)

you need to remove the brackets for it to be equal.

FALSE

[log_b(x)]^y = ylog_b(x)

let b=10, x=2, y=3

[log₁₀(2)]³ = 3log₁₀(2)

[log2/log10]³= 3log₁₀(2)

0.027 = 0.903

this is obviously not correct.

TRUE

log_b(x)^y = ylog_b(x)

ylog_b(x) = ylog_b(x)

This groups believes that because of the brackets, the equation is not correct and is a common error people can make. Since it's [log_b(x)]^y, you have to solve first and then put it to the power of 'y'.

If you don't agree with our solution, please post a comment on how you think it should be done. =)

be happy.

GROUP #2 : Ashlynn, Charlotte and Anh.

Is the following equation TRUE or FALSE?
Ln(A+B) = (LnA)(LnB)

Our answer is FALSE. We proved our answer by using an example.

ex: Let A=2 and B=3

Ln(2+3) = (Ln2)(Ln3)
Ln(5) = (Ln2)(Ln3)
(1.6094) = (.6931)(1.0986)
(1.6094) = (.7615)

Both sides of the equation do not equal each other, therefore the original equation is false.


A common error for this particular equation is that people may think they can go from Ln(A)Ln(B) to Ln(AB), but you can't because the logarithm laws do not allow you to do so.

So the correct answer would be:
Ln(AB) = Ln(A) + Ln(B)

Scribe Post: Day 10

Hi guys! This is Jann and I'll be your scribe for today.

As usual, we started our class with 3 problems.

Questions:

1. Find the inverse of each of the following:

a) f(x)= (x+3)/3

Solution:

i) Switch the y and the x variables.

y= (x+3)/3

x= (y+3)/3

ii) Solve for y.

3[x=(y+3)/3]3

3x= y+3

3x-3= y
f-1(x)= 3x-3

b) g(x)= ³√x-1

Solution:

y= ³√(x-1)

(x)³= [³√(y-1)]³

x³= y-1

x³+1= y

g-1(x)= x³+1

c) h(x)=1/x

Solution:

y= 1/x

y(x= 1/y)y

xy= 1

y= 1/x

Note: y=x is called an identity function. It means you get back what you started with. Since the inverse of this function is the same as it's original, it's considered to be a special function.

Note: If you feed the inverse of a function to itself, you'll always get "x" as an answer. [f(f-1(x))=x]

2. Given: f(x)= 3x/(x+5)

a) How do you know that "f" has an inverse?

Solution:

The easiest way to know if the function has an inverse is to simply graph it. The graph should look something like this:If this passes the horizontal line test, it means it has an inverse. Technically, it passes the line test.

b) Find the inverse of "f".

Solution:

Note: It was mentioned earlier that if an inverse of a function is fed to its original, the answer will always be "x".

f(f-1(x))= x

f-1(x){3f-1(x)/[f-1(x) +5]= x}f-1(x)

3f-1(x)= xf-1(x) +5x

3f-1(x) - xf-1(x)= 5x

f-1(x)*(3-x)=5x

f-1(x)= 5x/(3-x)

Note: We substituted "f-1(x)" as the unknown variable. After solving for "f-1(x)", we ended up with it's inverse: f-1(x)= 5x/(3-x).

3. f(x)= x^3 + 0.2x

a) Is "f" invertible?

Solution:

Note: Like in #2, we should graph the function to know if it is invertible. The graph should look like this:

The graph of this function is invertible because it passed the horizontal line test.

b) Sketch a graph with Domain [-1.5, 1.5] and Range [-1,1].

Note: To sketch this graph, we must adjust the window setting of the screen. To change the setting...

i) Press [WINDOW]

ii) Set "Xmin" to -1.5 and "Xmax" to 1.5

iii) Set "Ymin" to -1 and "Ymax" to 1.

iv) Finally, press [GRAPH].

You should have something like this:

c) Find f-1(0.45) to 2 decimal places.

Solution:

Note: To find the value of "f-1(x)", we need to trace it in the calculator. But first, we need to change our calculator setting to "Parametric". It describes what happens to x and y seperately.

i) Press [MODE]
ii) Arrow down to "Func" the arrow right to "Par". Press [ENTER]
iii) Press [Y=] then enter X1T= T.
iv) Enter Y1T= T^3 +0.2T
v) Press [GRAPH]

After entering the function, Press [WINDOW]. You'll see "Tmin","Tmax", "Tstep". Change "Tmin" to -1.5 and "Tmax" to 1.5

Note: "Tstep" is the calculation done by the calculator every pixel. f-1(0.45) is an "input", so we want the "output" of the function. If we trace the graph to x= 0.45, y should equal 0.18 to 2 decimal places.

Additional Problem: Find f-1(0.55)

Solution: Simply arrow right 2 times. You should see x=0.55, y=0.27

Lastly, if there is anything that's not explained properly, please give a comment.

I forgot to mention the method to draw the inverse of a function on the graph. Here are the steps:

i)Press [2nd] then [PRGM]
ii)Press [8] that says "DrawInv" then press [ENTER].
iii)The command will appear on the home screen. Press [VARS] then arrow right once then press [1].
iv) Press [Y1] (depends where you entered your function). Press [ENTER]

It should show you the inverse of the function you entered in [Y=].

I would also like to remind everyone that there "might" be a quiz tomorrow or on monday. Be ready.

Thats everything we talked about in class, I think. The next scribe is.... umm.... Christian. (^.^V)

Scribe Post: Day 9

Hey everyone, this is Suzanne. We started today’s class off with that quiz everyone had been looking forward to so very much. So I’ll start off by going over some of the methods Mr.K discussed for the first question, where we were asked to state how many roots the function had, and what the largest root was.

Unfortunately I don’t have the exact equation, so these graphs are an approximation. And not the greatest either. I'm no artist :p a) This function had two roots, but when you graph it on your calculator, it appears at first glance to have three roots. There are several ways to determine whether or not there is a root.

Method 1: First off, you can use the zero function on your calculator by pressing 2nd calc, zero. If the calculator comes up with a zero, then there’s a root there. But in this case, an error comes up saying ‘no sign change’. If this happens, then either there is no root, or the root touches the x-axis but does not cross it. This can be seen, for example, with the graph f(x)=x².

Method 2: So we still need to figure out whether there is a root or not. We can use the zoom-in function on the calculator, closing in on the root until we can clearly see whether it touches the x-axis or not. (I don't know if you can really tell, but I promise you that it's not touching the x-axis in this diagram. Cross my heart.)Method 3: Finally, we can find the minimum. Press 2nd, calc, minimum. The procedure from there is the same as if you were calculating a zero. (First pick a point to the left, then to the right). If the minimum value is greater than zero, then there is definitely no root. I personally think this is the most efficient way to complete the problem.

b) This function was very sneaky… it appears at first to have three roots. However, by looking at the equation we can tell that there are actually 4 roots. The highest exponent is even, so we know that both outer arms of the graph must go in the same direction. In this case, there was a negative sign in front of the function, so we know they point downward. Therefore there must be another root somewhere off to the right. We can find this root two ways.

Method 1: Expand the size of the window until you see the root. Then it is just a case of using the zero function on your calculator.

Method 2: Go to the table by entering 2nd, table and find the zero. Well, in this case it’s a nice prettyful zero at 50, but of course we will not always be that lucky. Just look for where the y-values go from positive to negative, and you will have a good idea where to look for the zero. Then it’s just a case of using method 1 to find your root.

I'm not going to go into the rest of the quiz, since I don't have the questions. After the quiz we started to talk about inverses, which is going to lead into a lesson on logs tomorrow (I think). First of all we discussed that exponents are the inverse of logs. Mr. K said that logs of base 10 and e are the most frequently used, and that after high school they are pretty much the only thing we will see. So here are some of the ideas we went over:

1) Find the inverse of the function:

We went over two ways of doing this.

Method 1: List step-by-step what is happening to x, then go through those steps from last to first, undoing whatever that step did.

and the function we end up with is:

Method 2) Switch x with y in the equation and then isolate y. You'll get the same answer as stated above. Note that this method won’t work on all functions. For example, f(x)= (2x-1)/(x+3) will not work. The reason for this is that 2 things are happening to x at once.

2) We have 2 functions: f(x)=2x+3 and g(x)= ½(x-3). What is f(g(x))?

f(g(x))= 2(1/2(x-3)) +3
= x-3+3
=x

In this case what you put in is what you get out. In other words, these two functions are inverses.

And that’s all I have guys. Stay tuned for tomorrow’s thrilling continuation! And the lucky winner of the ‘next scribe’ competition is…. Jann!

Scribe Post: Day 8

Hey kids, it's Loso and I was today's class scribe. Today we were given three questions to do, to follow up on what we learned yesterday [technically speaking, it's what you all learned yesterday because I wasn't in class yesterday, SORRY!].

QUESTIONS:

1. Dave invests $100 at 8% interest per year. How much does Dave have after 6 years if the interest is compounded;

a) annually
b) quarterly
c) continuously

2. The population of New Hampshire was 1 million in 1990. It doubles every 25 years. What is it today?

3. Describe all the features and properties of the graphs of:

a) y-2^x
b) y=3^-x

SOLUTIONS:

1. a) Since we're given a sufficient amount of information, we can use the A=P(1+r/n)^tn formula. I'm pretty sure you all know how to plug in the information, but just for every one's sake, let's make sure.

A is what we're looking for.
Our principle amount is $100 [P].
1 is taking 100% of what we already have and then adding it with the rate of interest.
Our rate of interest is 8%, and is 0.08 when written as a decimal [r].
6 is the amount of time we're looking at. [t]
n is the number of times we compound a year. In this case, we're compounding once every year.

A=P(1+r/n)^tn
A=100[1+(0.08/1)]⁽⁶⁾⁽¹⁾
A=100(1.08)⁶

We were able to leave it at that for today.

b) We use the same formula, with the exception that we're compounding 4 times a year, instead of once a year.

A=P(1+r/n)^tn
A=100[1+(0.08/4)]⁽⁶⁾⁽⁴⁾
A=100(1.02)²⁴

c)For c, we use A=Pe^rt

A=Pe^rt
A=100e^(0.08)(6)
A=100e^(0.48)

2. For this question, we use A=Ao(M)^t/p

A=Ao(M)^t/p
A=1,000,000(2)<sup>15/25

Umm, I kind of missed the answer. He was going through it pretty quickly. Hopefully I did that right.</sup>

3.

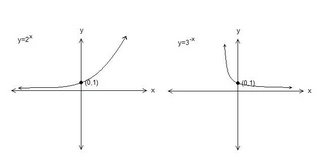
These are what the graphs look like.

y=2^x

-increasing function (or grows exponentially)
-asymptote is y=0
-DOMAIN (-∞, ∞)
-RANGE (0, ∞)
-y int. y=1
-no roots
-concaves up

y=3^-x

-decreasing function (or exponential decay)
-asymptote is y=0
-DOMAIN (-∞, ∞)
-RANGE (0, ∞)
-y int. y=1
-no roots
-concaves up

Everything in purple is what is similar between both functions.

We then discussed how to describe what an inverse was.

VERBALLY: An inverse of a function is a function that undoes what the parent function does. You can also say, the inputs become outputs, and the outputs become inputs

He brought up the baby play and parent clean up example. I think we're all pretty clear of what the point of that was.

NUMERICALLY: This was the example we were given, basically showing how the y values become x values, and the x values become y values.

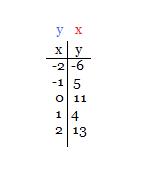
GRAPHICALLY:

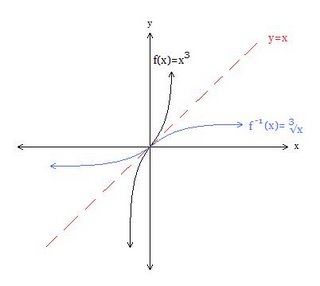
Yeah, I know the lines look wrong, but it's the best I can do right now so bear with me. Near the end of the class, there was some discussion about one to one functions, which at this time is quite vague to me. It's late and my brain needs rest. Our homework is exercise 1.6, all odd questions including 10,18,28 and 30.

For the next scribe, I choose Suzanne. Have fun with that. =)

Scribe post: Day 7

Hey everyone my name is Ashlynn and I will be your scribbler for today =D. Sorry if I was late on my scribe, I lost my first version and I had to start all over, and it frustrated me a bit. But it's okay now =) . Today's class began with a talk about which scribes belong in the Hall of Fame. Well class began with these questions:

1) If the graph of a function of the form y = Ce^rt passes through the points (0,3) and (2,7), determine the constants C and r.

I started by plugging the value (0,3) into the equation y = Ce^rt;
* The input value is 0, which is t, and the output value is 3, which is y. So I just substituted them into the equation*
3 = Ce^r0

Anything raised to a 0 equals 1 so e^r0 = 1.

3 = C(1)

therefore;

C=3

To solve for r, we start by using C = 3 and the points (2,7) into the equation.

7 = 3e^r2

7/3 = e^r2

Take the natural log of both sides

ln (7/3) = 2r lne

We know that ln e = 1. ln e = 1 because ln e=loge e ( I don't know how to make subscripts so bare with me =) ) Base e raised to the power of e is one. This is a rule that applies all the time. I understand what this is about, but I am having difficulty explaining it, so please be free to leave a comment.
ex) log5 5=X
5^x = 5
5^x = 5¹

Now back to our question;

ln(7/3) = 2r
(1/2) ln(7/3) = r

so, r = .4236489302 , but we can round it off to four decimal places

r = .4236

2) Six months after some laboratory rats were delivered to a new research lab, there were 786 rats present. Nine months after the original delivery there were 1720 rats. Assuming exponential growth for the rat population, how many were in the original delivery?

The equation we use is P=P _o(model)^t

We know,
P₆ = 786 t = 6
P₉ = 1720 t = 9
P₀ = ?

change in t = 9-6
= 3

We let Po = 786 then t=3. Plug these values into the equation P=P_o(model)^t

1720 = 786 (model)³

1720/786 = (model)³

Now we use natural log because it deals with population. Populations grow continuously, and that is why we use base e.

ln(1720/786) = 3 ln(model)
(1/3) ln(1720/786) = ln(model)

* *remember when using your calculator to find the answer remember to store your answer*
Sto --> , Aplha A

ln(model) = 0.2610409258 , we can round it to 4 decimal places.

model = e^.2610

Our equation is P = 786e^.2610t

Okay now we found our model now we have to find the original value. There are 2 methods.

Method 1:

P = 786e^.2610t , but we are looking for six months before so t = -6

P_-6 = 786 e^.2610(-6)

P_-6 = 164

Method 2:

Let P₆ = 786

786 = P_oe^.2610(6)

786/e^.2610(6) = P_o

164 = P_o

Homework for tonight is 1.5 in the textbook, odd numbered questions, and to sign up for an account on the websites Mr. K provided in the previous post.

This was pretty much what we did today. I hope my work was clear and easy to understand. Please be free to make any corrections if something is unclear. I'll be happy ot fix it. The next person I pick for Scribe is Loso.