Developing Expert Voices - Invitation to the Blog

As promised, I built a unique blog for your Developing Expert Voices projects. Email me and I will send you an invitation to the new blog. When you publish your projects on the DEV blog tag them with the name of your class (AP Calculus) and the topics covered by the problems you created.

You can take a sneak peak at the new blog here.

Click that picture ... there's a great article at the other end of that link.

BOB

Hi! My BOB's a bit late, because I haven't done the test yet. It's 11pm of Monday, March 26th right now, and I just finished a couple of calculus questions. That tells you how boring my life is when it's the first day of Spring Break, and of all things, cALcuLus is in my head. Well, it's because of the anxiety some people have expressed on Friday by the people who have taken the test. They said it was very difficult and they had a hard time doing it. I thought I had the main ideas down, but according to a few classmates, that wouldn't be enough.

This is my gameplan:

I'll try to come up with a step-by-step method in solving these problems. These are integral questions still right, but see, I still have problems with integrals. I'm not super duper comfortable with them yet. If there's a step-by-step method with the problems, I think it'll help me. Sometime when we come back to school, I'll probably stop by Mr. K's room to ask for help. Til then!

Developing Expert Voices Rubric out of beta v.1.0

This is the final version of the document we built together.

---

Developing Expert Voices Rubric

The teaching of mathematical concepts is the main focus of this project; so we can teach other people and learn at the same time.

Acheivement Descriptors
Instead of levels 1-4 (lowest to highest) we use these descriptors. They better describe what this project is all about.
Novice: a person who is new to the circumstances, work, etc., in which he or she is placed; a beginner.
Apprentice: to bind to or place with a master craftsman, or the like, for instruction in a trade.
Journeyperson: any experienced, competent but routine worker or performer.
Expert: possessing special skill or knowledge; trained by practice; skillful or skilled.

Acheivement	Mathematical Challenge (25%)	Solutions (55%)	Presentation (20%)
Novice	Problems illustrate only an introductory knowledge of the subject. They may be unsolvable or the solutions to the problems are obvious and/or easy to find. They do not demonstrate mastery of the subject matter.	One or more solutions contain several errors with insufficient detail to understand what's going on. Explanation does not "flow," may not be in sequential order and does not adequately explain the problem(s). May also have improper mathematical notation.	Presentation may or may not include visual or other digital enhancements. Overall, a rather uninspired presentation. Doesn't really stand out. It is clear that the student has invested little effort into planning their presentation.
Apprentice	Problems are routine, requiring only modest effort or knowledge. The scope of the problems does not demonstrate the breadth of knowledge the student should have acquired at this stage of their learning.	One or more solutions have a few errors but are understandable. Explanation may "flow" well but only vaguely explains one or more problems. Some parts of one or more solutions are difficult to follow. May include improper use of mathematical notation.	The presentation style is attractive but doesn't enhance the content; more flashy than functional. It is clear that the student has invested some effort into planning their presentation.
Journeyperson	Not all the problems are "routine" in nature. They span an appropriate breadth of material. At least one problem requires careful thought such as consideration of a special case or combines concepts from more than one unit. Showcases the writer's skill in solving routine mathematical problems.	All solutions are correct and easy to understand. Very few or no minor errors. Explanation "flows" well and explains the problems step by step. Solution is broken down well and explained in a way that makes it easy to follow. May have minor use of improper mathematical notation. May point out other ways of solving one or more problems as well.	The presentation may use multiple media tools. The presentation style is attractive and maintains interest. Some of the underlying message may be lost by some aspects that are more flashy than functional. It is clear that the student has given some forethought and planning to their presentation.
Expert	Problems span more than one unit worth of material. All problems are non-routine. Every problem includes content from at least two different units. Problems created demonstrate mastery of the subject matter. Showcases the writer's skill in solving challenging mathematical problems.	All solutions correct, understandable and highly detailed. No errors. Explanation "flows" well, explains the problems thoroughly and points out other ways of solving at least two of them.	The presentation displays use of multiple media tools. The presentation style grabs the viewer's or reader's attention and compliments the content in a way aids understanding and maintains interest. An "eye opening" display from which it is evident that the student invested significant effort.

Creativity (up to 5% bonus)

The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:

• unique and creative way of sharing student's expertise, not something you'd usually think of;
• work as a whole makes unexpected connections to real world applications;
• original and expressive;
  
• imaginative;
• fresh and unusual;
• a truly original approach; presentation method is unique, presented in a way no one would expect, e.g. song, movie, etc.
  

BOB

This unit was about finding the definite integral. I understood most of it in the beginning, but then I started getting confused near the end. I should have went to class more, but that was my fault. I crammed all night and attempted some of the questions. But I'm still not confident in how well I'll do the test this morning. Well hopefully the lunch classes will help me for the big exam. Good luck everyone!

BOB

This unit was pretty quick. I understood most of what we were learning in class. The only thing I have trouble with if figuring out the image with the shells and all. The picture is what I get mixed up on, then my answer's wrong. In class today, I understood it, so I was happy. I liked this unit. I don't really like the word problems, again because of picturing the problem and the graph. I don't like the density problems I get confused easily. I didn't do very well on the pre-test. It was a lot of guessing. When Mr. K explained it all, it seem so simple. I usually think that it's more complicated than it really is. So I end up doing all this funky complicated stuff. This week was very, very busy. I had four other tests (this one's the last =D!), essays, and articles to do. So, that didn't really help. I'm soooo glad Spring Break is coming up!!

BOB

Right now I'm working on the supplementary problems for this chapter, and so far so good. I had some trouble on the pretest yesterday, I think mainly because I didn't practice the different types of problems as much as I should have, so I forgot how to solve them after a few days. But yesterday and today has refreshed the basics of this chapter a little, so I think I can manage tomorrow. I was a bit confused by the density problems, and haven't really tried any outside of class yet, so that's my plan for the immediate future. And I want to work on the average value and mean value stuff too. (Though we didn't do much with the mean value thing, so I don't know if it'll even be on the test.) I have three tests tomorrow though and I still have to study for one of them... but hey, get through tomorrow and it's spring break :) Good luck everyone! Have a nice spring break, preferably homework-free.. preferably somewhere with sandy beaches and no snow.

BOB the Snail

Hi everyone! Our unit on Integral Applications is done and we're going to have a test. This unit has been really short. I found this unit easier to understand than the unit before this. The applications are fairly straight forward. We just need to practice these problems. Why BOB the Snail? A snail is a very slow creature. It's having difficulty in crawling from one place to another; but it never gives up. Like us, we should never give up on our studies. Even though I feel like falling behind, I still think about "going for it".

Good luck on the test everyone! XD

BOB

BOB,

To be completely honest, I do not understand this unit. I hear everything that's being said in class, and during that time, I think I understand. When I leave the class, WHOOSH, it's all gone. Why? Maybe it's because in calculus class, you have to think about it, so you understand it. It's fresh in my mind. When I leave the room, I walk into a world where you have to think about many other things and all that calculus knowledge is pushed back into the dark corner of a filing cabinet...which MAY or MAY NOT come back. This unit is supposed to be the fun part of calculus but I'm really not enjoying it. It could be because I don't understand it, I can't picture what the graphs look like. The paper towel and washer analogies are helpful, but to me, it doesn't have a purpose.

I wish, like many of my fellow classmates, that we had more time to study. It's late in the year, we're tired. We need to recharge our batteries. Tomorrow is the test and honest to goodness, I am more afraid of this test than the AP exam. I really am. There are bits and pieces that I do understand, but I just can't use them to get the whole picture.

Good luck to my classmates. After this test, we could relax, Spring Break is so near, I can feel it. I wish we had more time to study x 2. Tests are supposed to show how well you understand a topic...but if we really don't understand, I don't think it's beneficial to have one. If we don't understand this unit, we will struggle in the next unit. Spring break, spring break, spring break.

Ohhh my BOB

Dear Bob,

As you may already know, we've been having lunch hour classes, because we're behind in the curriculum. The exam is in the beginning of May, which is really just around the corner. Hmm.. you see, I took AP Calc for the experience and as a challenge. And so far, it really has been a challenge.

This unit was really easy to follow and understand in the beginning. But as we progressed, I had diffuculty in picturing what the arbitrary slice would look like when taken from the solid. They come in disks, washers, and prisms depending where you rotate them. To find the volume, you need to find the volume of one slice by finding its area. The only thing that varies is the radius, and I think its true, how knowing what the radius represents is the tricky part of it. Once you have the integral, the rest is just a matter of punching into the calculator. I don't know why, but I understand things when we do it in class... when it came to the pretest, I thought too hard about it. It was simpler than I thought. It sometimes frustrates me, because I should know better... I do know better.

I wish I had more time to study. I have another test to study for, a pile of homework to do, a book to finish reading, and other things to take care of. Nonetheless, don't we all wish we had more time? If we could rewind and do it better, put more effort, DO not some, but ALL of the homework, would we not? Yes, the test is tomorrow.. but that is the beauty of AP Calc.. because now, if and when we take it in University, we can remember what it felt like when we weren't prepared and we can laugh... because by then, we'll have learned our lesson and know better.

Biiig siiiigh.. the test is tomorrow!!! But you know what that means.. SPRING BREAK is on its way.. and it's getting nice out! WOOHOO... one more unit and we're done, done, done. When you think of giving up, just remember Sisyphus. Good luck to all and to all a good night =)

BOB #8

This unit started off easy and towards the end it got harder. I think that's the way all the units were. At the beginning I did the homework and then stopped because I thought I already knew what I was doing. When the pretest came, it hit me that I didn't quite know what I was doing and right now I feel like I need to do the last chapters so that for the test tom. I feel confident enough to complete the questions. I think its going to be tough for me but I'm still going to try. I need to do more questions about when the function spins around the y-axis and at different values. I'm not quite sure about those. Good luck to everyone and be happy b/c remember it's spring break next week! =)

Today's Slides, Review and Worksheet: March 22

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

And here is the worksheet ...



and (some of) the answers ...

BOB

well, im not sure this unit is kind of weird. i am having a hard time seeing how a function would look like if we spin it around an axis. on the multiple choice, i noticed they were questions similar to what we did in the beginning of the unit. For example, the first question that dealt with wrapping the function around y= -1. i actually found the rate multiple question easier (last question on first page). must be careful with those itty bitty pieces.

Blogon the Blog #8

The pre-test was hard. This unit is pretty tough! But once you get around how to find the integral, which pretty much is the hard part, then it becomes mechanical from there. I think my biggest problem is deciding whether or not the solid volume produce spinning a function around the y or x axis is going to be a cylindrical shells, or round discs.. when the y or x axis you're spinning it about is translated units. But I think by doing more problems like these, I could surely get it. I've been focusing my attention to another subject that is of much greater value to me and resulted in less time for calculus. After spring break, everything should be fine.

Today's Slides: March 21

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Scribe Post 90

First off, i would like to remind everyone to go and add to the marking rubric for our project. Rubric is due this Friday.

1) Oil is leaking at a rate of R(t) = 2000e^-0.2t
, where t is measured in hours, how much oil has spilled in 10 hours?


We want to end up in gallons, so we multiply gallons per hour (which we are given) by some change in time. We want to find the total sum over the ten hours.
*When we are given a rate, such as the one above, we are trying to find a unit related to the rate. I.e. (gallons/hour)x(hour) = gallons.*


A) Density of an oil slick on a body of water is defined by

Suppose the oil slick is extends from 0 to 1000 m. Determine the mass of the slick.
We have Kg/m² and we want to get kg, so we have to get rid of the m²

We cut a piece from the oil slick. If we drill down, the density of the oil slick is the same throughout.

Here we have cut a piece out of the oil slick. The ends of the strips (triangles) become smaller. So we take the triangle and move it to one side to form a rectangle. The area of the rectangle is what we need to find. Going back to our equation we can now get rid of m²

With our our information and our missing piece found, we can create an integral to solve for the mass of the oil slick. We take the limit of n as it approaches infinite and it becomes smaller. We can then take the sum, where n equals one. p(a) is our given equation so we multiply that by the rectangle piece we cut out, Am². Then we get the integral from 0 to 1000 meters. 100/(1+r²) is kg/m² multiplied by 2pi r dr m², which will give us the mass of the oil slick 1000 m out. 2pi r is multiplied by dr because dr becomes infinitely smaller.
*check the slide for march 19 to view the solution to the integral*

B)What is the smallest radius that contains 75% of the oil slicks mass?
With our solution from A, all we do is take seventy percent of the value we found. We can then pull out 200pi. From here we just solve for r, by expanding the bracket notation first.

For the last part of class, we talked about how our physics formula can be derived. We also did a quick question before the bell rang. We were given an amount of cars per kilometer. instead of trying to cancel out a unit area we had to cancel a length to get the number of cars.


URGH, i got a cold.... next scribe is Suzanne... pre test tmrw?

Today's Slides and Homework: March 20

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

A Second Wind?

"Most people never run far enough on their first wind to find out they've got a second. Give your dreams all you've got and you'll be amazed at the energy that comes out of you." --William James

I wonder, would this apply to calculus too?

Today's Slides: March 19

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

SCRIBE POST: DAY 89

The plan was to have this up by Friday. Sorry guys. Anyway, I haven't been scribe for quite some time, so it took me awhile to get back into it...

We started class by talking about our due dates for our DEVELOPING EXPERT VOICES assignment. Remember guys: you can always move your due date earlier than expected. We also talked about the rubric for this assignment. Remember that changes must be made no later than Friday, March 23rd.

Let's get the math started...
To solve for a you simply plug in 1 for k. To solve for b, c, and d, you must integrate it from 1 to the number of items. We start with 1, because this is where the domain of the function begins. If you plugged 0 into the function, you would get 23 minutes. This doesn't make sense; it shouldn't take 23 minutes to make nothing. Once you know the integral, the rest is just punching it into the calculator. The answers can be found on the bottom of this page. https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjKDzv2OOobRwicccwEDRidnFn0ZXsphtj3GaokY2BSlnEC23kRzA8syG4oaBXJoiiFeJXCaYzuylt93wtfbXQbCu861Hn1WdeEdoWRFt4goN56ek7EOiEEVv110iM7uUYrK5oCYxmsrcM/s1600-h/AppsOfTheIntegralExerc.jpg Note: This is a good exercise to practise for the unit test.

With the help of Fooplot http://www.fooplot.com/, we were able to see what the graph looked like. Points of intersection tell you where to integrate.

1. To find the area of S, we simply find the integral from 0 to 4. Because the function f(x) is on the bottom, we subtract it from g(x).

2. To find the volume of S, we first find the volume of one piece. We take an arbitrary slice, and find its area. In this case, the shape of the slice is a semi-circle, where the radius is the top function, g(x), subtract the bottom function, f(x). Once you have the area, you must write the integral. You then apply this integral to find the volume of the whole thing.

3. Because we S is rotating, you can imagine a solid being formed with a hole in the middle. To find the area, we must take the area of the smaller circle and subract it from the area of the bigger circle. Questions a, b, and c are all the same question; the only difference between them is how the radii are formed.

a)


b)

c)

d) In this case, the solid is rotating around the y-axis, therefore the shape of the arbitrary slice is no longer a circle. It becomes a prism. The width of the prism is the circumference. (remember: the paper towel) Its thickness is dx, because we want the slice to be infinitesmally small. Its height is simply the top function, g(x), subtract the bottom function, f(x).

So that brings us to the end. If you're still having trouble, the slides from Thursdays class http://www.slideshare.net/gofull/30241/1 are up.. thank goodness for our super-di-duper smartboard!!! HMWK for the weekend is EXC 8.5 # 1,3,5,11,15. And by the way, MARK is the scribe for Monday! Enjoy the rest of your weekend guys =)

Today's Slides and Homework: March 15

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Also, here is a practice set of "applications of the integral" problems.

Pi Day

Happy π Day!

Developing Expert Voices

The Assignment
Think back on all the things you have learned so far this semester and create (not copy) four problems that are representative of what you have learned. Provide annotated solutions to the problems; they should be annotated well enough for an interested learner to understand and learn from you. Your problems should demonstrate the upper limit of your understanding of the concepts. (I expect more complex problems from a student with a sophisticated understanding than from a student with just a basic grasp of concepts.) You must also include a brief summary reflection (250 words max) on this process and also a comment on what you have learned so far.

Timeline
You will choose your own due date based on your personal schedule and working habits. The absolute final deadline is May 31, 2007. You shouldn't really choose this date. On the sidebar of the blog is our class Google Calendar. You will choose your deadline and we will add it to the calendar in class. Once the deadline is chosen it is final. You may make it earlier but not later.

Format
Your work must be published as an online presentation. You may do so in any format that you wish using any digital tool(s) that you wish. It may be as simple as an extended scribe post, it may be a video uploaded to YouTube or Google Video, it may be a SlideShare or BubbleShare presentation or even a podcast. The sky is the limit with this. You can find a list of free online tools you can use here (a wiki put together by Mr. Harbeck and myself specifically for this purpose). Feel free to mix and match the tools to create something original if you like.

Summary
So, when you are done your presentation should contain:
(a) 4 problems you created. Concepts included should span the content of at least one full unit. The idea is for this to be a mathematical sampler of your expertise in mathematics.

(b) Each problem must include a solution with a detailed annotation. The annotation should be written so that an interested learner can learn from you. This is where you take on the role of teacher.

(c) At the end write a brief reflection that includes comments on:

• Why did you choose the concepts you did to create your problem set?
• How do these problems provide an overview of your best mathematical understanding of what you have learned so far?
• Did you learn anything from this assignment? Was it educationally valuable to you? (Be honest with this. If you got nothing out of this assignment then say that, but be specific about what you didn't like and offer a suggestion to improve it in the future.)

Experts always look back at where they have been to improve in the future.

(d) Your presentation must be published online in any format of your choosing on the Developing Expert Voices blog. url: tba.
Experts are recognized not just for what they know but for how they demonstrate their expertise in a public forum.

Levels of Achievement
Instead of levels 1-4 (lowest to highest) we will use these descriptors. They better describe what this project is all about.

Novice: A person who is new to the circumstances, work, etc., in which he or she is placed.

Apprentice: To work for an expert to learn a skill or trade.

Journeyperson: Any experienced, competent but routine worker or performer.

Expert: Possessing special skill or knowledge; trained by practice; skillful and skilled.

Happy Pi Day!

Click here to view the card Lani has sent you!

Scribe Post

Good day ya'll! This is Jann and I'll be your scribe for today.

Today, we learned how to find the Average Value for Functions.
We started by getting the average value of a set of numbers.

8 +5 + 7 + 7 + 3 = 6
5

Here's the definition of the Average value of a Function:
"Let 'f' be a function which is continuous on the closed interval [a,b]. The average value of 'f' from x=a to x=b is the integral...

Q: Where did this formula come from?

A: Good question! If we examine a graph of any function, we can say that "a" is the lower limit of the graph and "b" is the upper limit of the graph.

This is the formula used to find the width of the intervals."x" is the width of the intervals. If we recall, we divide the graph of a curve into rectangular divisions to find the area under the curve. "x" varies because the more the intervals, the width of the intervals will decrease. "n" is the number of intervals used to divide the curve.

If we try to solve for "n", we need to rearrange the formula.

According to our Average Value rules, we need to add all the outputs and divide it by the number of intervals used. Therefore... We substituted the formula for n in the denominator. The formula boxed in red is the Riemann Sum. The "E" symbolized the summation of all the outputs in the function, "f". "x" is a constant since the width of an interval never changes. The number of intervals will go to infinity to get the area under the curve. The limit and the summation are symbolized by the integral from [a,b].

Example:

Find the average value of the given function on the given interval.

f(x) = 1 - 2x [0,3]

Using the average value formula for functions, we can get the average value...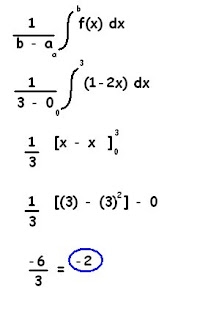

Then, we talked about the Mean Value Theorem for Integrals.

If we recall, the Mean Value Theorem for Derivatives state that: Let f be continuous on a closed interval, [a,b]. There lies a value "c" that is equal to the rate of change of the curve.

The Mean Value Theorem for Integrals state that: Let f be continuous on a closed interval [a,b]. Then there exists "c" in the closed interval such that...

With all that said and done, we practiced 1 problem.

Find the i) average value of "f" on the given interval, ii) "c" such that the average of "f" is equal to the f(c), and iii) sketch the graph of f and a rectangle whose area is the same as the area under "f".

f(x) = 2x [0,3]
I think that's all we did in class. Next scribe is... err.... I'm not sure who to pick. XD I'll just pick during the next class.

Today's Slides and Homework: March 13

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Also, here is a practice set of "average value of a function" problems.

Scribe Post

HI Everyone!! Here's the post for friday's class:

On friday, we started with a non-calculator quiz then did we did the following lesson:

Note: If pics hard to see, just click on pic so its bigger.




_____________________________________


____________________________________



Homework: Ex. 8.3 odd #'s

Next Scribe is going to be Jann =D

Today's Slides and Homework: March 12

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Also, here is a practice set of volumes of revolution problems.

Today's Slides: March 9

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Scribe Post

Finding the Volume of a Solid
(note: The pics aren't as clear, so please just click on them for a better view)

Imagine a rectangular, three-dimensional solid. To take the volume of this figure, we multiply its thickness, height and width together.

V = (thickness)(length)(width)

Another way to find V is if we divide the solid into even figures, find the volume of one of the smaller pieces, and multiply it by how many smaller pieces there are. In other words:


Volume has three dimensions, and Area has two. By integrating, we are essentially finding the thickness of an object. Going back to the equation V = (thickness)(length)(width), one dimension is already accounted for. We only need to find two more, and this is the area of the cross section.

In general, any function rotated around the x-axis will have circular cross sections, and its volume can be found by:

A(x) is the function representing the changing areas. The area for all the cross sections is represented by A = πr², but r varies, so we need a function that represents r.

Let’s take a look at an example:


Imagine a line segment from the point (0, 4) to (8, 0). Revolve this line on the x-axis, and you’d get a cone, as seen in the diagram below. To find the volume, let’s follow the steps we learned in class:

(1) Find the function that represents the radius.
(2) Replace “r” with this function in the “volume equation” up there.
(3) Integrate over the interval.



If we compare this to what we get if we use the geometric equation we’ve used in elementary (V = 1/3πr²h), we get the same answer!!

So there you go folks. I think the three steps are doable. Homework is Exercise 8.2 ODDS. Scribe is JANN!

Today's Slides: March 7

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Scribe Post

Hi guys :) Yesterday we started unit 8.

First off we started with a few problems which you probably recognized from past units.

Find the area bound by the two curves:

To solve these, you must look at the graphs, and determine which function is above and which is below. Then you take the integral of the top function minus the bottom function. To find the interval, make the two functions equal each other and solve for x.





After that we discussed a problem where we are given a velocity function and asked to find the displacement, also known as net distance, and total distance travelled. The net distance is found by subtracting the negative integrals from the positive integrals. The total distance travelled is found by taking the integral of the absolute value of v(t).




That's all you need to know to do excercise 8.1.

Then we started to discuss how a 3 dimensional object is created by 'spinning' the function around the x axis (or y axis, but we didn't get into that just yet). We discussed how you can take many 'slices' of the solid, so thin that the width approaches zero. I guess we'll be expanding on this in class tomorrow.

The rest of the assigned homework includes the odd questions from 1-7 of exercise 8.2.

The scribe tomorrow shall be...... Danny.

More about ants ...

I just stumbled upon this. After Lani's recent post I thought it might be interesting to all of you ...



To view the slides in full screen mode go here and click on the [full] button in the bottom right hand corner of the slideshow.