



An interactive learning ecology for students and parents in my AP Calculus class. This ongoing dialogue is as rich as YOU make it. Visit often and post your comments freely.
 In order to solve this problem, we need to find the parent function. dy/dx is some constant multiplied by the parent function. We know that the temperature, T, varies with respect to time. (Basically, the temperature of the roast decreases over time) We need to find 2 points on the parent function...
In order to solve this problem, we need to find the parent function. dy/dx is some constant multiplied by the parent function. We know that the temperature, T, varies with respect to time. (Basically, the temperature of the roast decreases over time) We need to find 2 points on the parent function...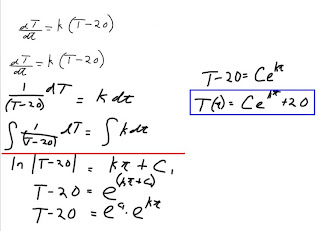 Then, after acquiring the 2 points in the parent function, we integrate the formula. The Red Line shows that the calculus part of the problem ends. The following line is all Pre Calculus stuff. If we can recall our natural law from Grade 12 PreCal, "kt + C" is an exponent. Therefore, it is an exponent of the base "e". "e^C1" can be substituted into "C" because it is a constant. Then, we isol
Then, after acquiring the 2 points in the parent function, we integrate the formula. The Red Line shows that the calculus part of the problem ends. The following line is all Pre Calculus stuff. If we can recall our natural law from Grade 12 PreCal, "kt + C" is an exponent. Therefore, it is an exponent of the base "e". "e^C1" can be substituted into "C" because it is a constant. Then, we isol ate the "T" in order to obtain the Parent Function.
ate the "T" in order to obtain the Parent Function.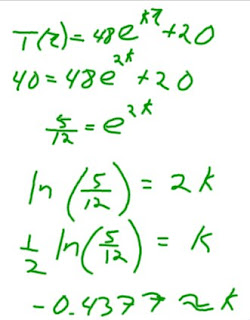
 Now that we have the parent function. We are ready to solve the problem...
Now that we have the parent function. We are ready to solve the problem... Then, we looked at one more example...
Then, we looked at one more example...

 That's all we did today in class. We were suppose to look at another example, but we ran out of time. Good day everyone! XD
That's all we did today in class. We were suppose to look at another example, but we ran out of time. Good day everyone! XD The order of a differential equation is the highest-order derivative.
The order of a differential equation is the highest-order derivative.

 We have Kg/m2 and we want to get kg, so we have to get rid of the m2
We have Kg/m2 and we want to get kg, so we have to get rid of the m2 


With the help of Fooplot http://www.fooplot.com/, we were able to see what the graph looked like. Points of intersection tell you where to integrate.
So that brings us to the end. If you're still having trouble, the slides from Thursdays class http://www.slideshare.net/gofull/30241/1 are up.. thank goodness for our super-di-duper smartboard!!! HMWK for the weekend is EXC 8.5 # 1,3,5,11,15. And by the way, MARK is the scribe for Monday! Enjoy the rest of your weekend guys =)




















 Use substitution. (I FORGOT TO PUT dx INTO THE PICTURE)
Use substitution. (I FORGOT TO PUT dx INTO THE PICTURE)



 If the 8 was a 9 in the polynomial we could complete the square.
If the 8 was a 9 in the polynomial we could complete the square. Next we use substitution.
Next we use substitution.
