1) The rate at which ice is melting in a pond is given by dV/dt =
a) 7.60
b) 7.62
c) 7.64
d) 7.66
e) 7.68
Solution: There's several ways you can come about this but I think the easiest would be to use "MATH", "9: fnInt(". Make sure you're calculating between the interval [0, 3] for the first 3 minutes.
2) The velocity of a car in miles per hour is given by v(t) = 80sin(t²) for 0 ≤ t ≤ 1. The approximate distance traveled from t = 0 to t = 1 is:
a) 20 miles
b) 25 miles
c) 30 miles
d) 35 miles
e) none of these
Solution: Once again I think "MATH", "9: fnInt(" is the easiest thing to use to solve this, only this time you're using the interval [0,1].
3) Which of the following statements is true?
a) If f" (0) = 0, then the graph of f changes concavity at x = 0.
b)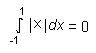
c) If the graph of a function is always convave up, then the left-hand sums are always less than the right-hand sums, with the same subdivisions, over the same interval.
d) If the function f is continuous on the interval [a, b] and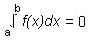
, the f must have at least one zero between a and b.
e) If f ' (x) > 0 on an interval, then the function f is concave up on the interval.
4) Water flows into a tank at a rate of (5t + 4) gallons/minute where t is measured in minutes and at the same time water flows out of the tank at a rate of 0.5t² gallons per minute. If at t = 0, the tank contains 10 gallons of water, what quantity of water will be in the tank at t = 4?
a) 40 gals
b) 45 gals
c) 50 gals
d) 55 gals
e) none of these
Solution: This also can be solved in different ways, the way I found most easiest was using "MATH", "9: fnInt(". You first find the integral of (5t + 4) at the interval [0, 4] then add 10 gallons to that answer because your tank starts 10 gallons. Then you find the integral of 0.5t² at the interval [0, 4]. Take the second answer and subtract it from the first answer to get your solution.
5) Two cars start from rest at a traffic light and accelerate for several minutes. The figure below shows their velocities as a function of time. Which of the following statements are true? (NOTE: there is no graph right now, I WILL have one up soon.)
b)
c) If the graph of a function is always convave up, then the left-hand sums are always less than the right-hand sums, with the same subdivisions, over the same interval.
d) If the function f is continuous on the interval [a, b] and
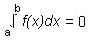, the f must have at least one zero between a and b.e) If f ' (x) > 0 on an interval, then the function f is concave up on the interval.
4) Water flows into a tank at a rate of (5t + 4) gallons/minute where t is measured in minutes and at the same time water flows out of the tank at a rate of 0.5t² gallons per minute. If at t = 0, the tank contains 10 gallons of water, what quantity of water will be in the tank at t = 4?
a) 40 gals
b) 45 gals
c) 50 gals
d) 55 gals
e) none of these
Solution: This also can be solved in different ways, the way I found most easiest was using "MATH", "9: fnInt(". You first find the integral of (5t + 4) at the interval [0, 4] then add 10 gallons to that answer because your tank starts 10 gallons. Then you find the integral of 0.5t² at the interval [0, 4]. Take the second answer and subtract it from the first answer to get your solution.
5) Two cars start from rest at a traffic light and accelerate for several minutes. The figure below shows their velocities as a function of time. Which of the following statements are true? (NOTE: there is no graph right now, I WILL have one up soon.)
I) Car 1 is ahead at one minute.
II) Car 2 is ahead at two minutes.
III) Car 1 and Car 2 are accelerating at the same rate at t = 1.
a) I only
b) I and II only
c) II and III only
d) I and III only
e) I, II, III
6) The rate at which our domestic oil supply is being consumed is continuously increasing. Suppose the rate (in barrels per year) is given by the function r = f(t) and t = 0 is the start of 1992.
6) The rate at which our domestic oil supply is being consumed is continuously increasing. Suppose the rate (in barrels per year) is given by the function r = f(t) and t = 0 is the start of 1992.
a) Write a definite integral that represents the total quantity of oil used between the start of 1992 and the start of 1996.
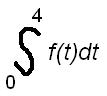
b) Suppose f(t) = 16e0.04t. Using left-hand sum with four subdivisions, manually find an approximate value for the total quantity of oil used between the start of 1992 and the start of 1996.
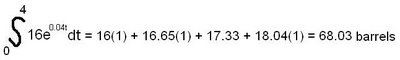
c) Interpret each of the four terms in the sum from part (b) in terms of oil consumption.
Each of the four terms you find for part (b) is the least number of barrels used in that year because you're finding the left-hand sum.
That's about all from today's class, we were suppose to have the test tomorrow but when Mr. K asked us if we were ready for it tomorrow we all responded with a resounding NO =P So we shall discuss it as a class tomorrow to see if we should have it Friday or Monday. No homework tonight however you should review the textbook, notes, exercises, scribe posts and the websites tagged for delicious for more studying!
Sorry this is up soooooooooo late and the next scribe will probably not be able to see this so.....CHRISTIAN! IF YOU DON'T SEE THIS NOW, I SHALL TELL YOU TOMORROW. I wonder what your reaction will be? Once again extremely sorry.
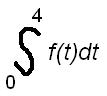
b) Suppose f(t) = 16e0.04t. Using left-hand sum with four subdivisions, manually find an approximate value for the total quantity of oil used between the start of 1992 and the start of 1996.
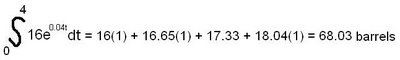
c) Interpret each of the four terms in the sum from part (b) in terms of oil consumption.
Each of the four terms you find for part (b) is the least number of barrels used in that year because you're finding the left-hand sum.
That's about all from today's class, we were suppose to have the test tomorrow but when Mr. K asked us if we were ready for it tomorrow we all responded with a resounding NO =P So we shall discuss it as a class tomorrow to see if we should have it Friday or Monday. No homework tonight however you should review the textbook, notes, exercises, scribe posts and the websites tagged for delicious for more studying!
Sorry this is up soooooooooo late and the next scribe will probably not be able to see this so.....CHRISTIAN! IF YOU DON'T SEE THIS NOW, I SHALL TELL YOU TOMORROW. I wonder what your reaction will be? Once again extremely sorry.
1 comment:
this is a GREAT post. YOu have everything a reader needs. Great use of colour, images and tons of detail. I like your solutions and how you mention that there are different ways to solve the problems. It is clear to your audience that you put a lot of effort into this scribepost. Thanks for taking the time.
Mr. Harbeck
Sargent Park School
Post a Comment