Scribe Post

Good day ya'll! This is Jann and I'll be your scribe for today.

Today, we learned how to find the Average Value for Functions.
We started by getting the average value of a set of numbers.

8 +5 + 7 + 7 + 3 = 6
5

Here's the definition of the Average value of a Function:
"Let 'f' be a function which is continuous on the closed interval [a,b]. The average value of 'f' from x=a to x=b is the integral...

Q: Where did this formula come from?

A: Good question! If we examine a graph of any function, we can say that "a" is the lower limit of the graph and "b" is the upper limit of the graph.

This is the formula used to find the width of the intervals."x" is the width of the intervals. If we recall, we divide the graph of a curve into rectangular divisions to find the area under the curve. "x" varies because the more the intervals, the width of the intervals will decrease. "n" is the number of intervals used to divide the curve.

If we try to solve for "n", we need to rearrange the formula.

According to our Average Value rules, we need to add all the outputs and divide it by the number of intervals used. Therefore... We substituted the formula for n in the denominator. The formula boxed in red is the Riemann Sum. The "E" symbolized the summation of all the outputs in the function, "f". "x" is a constant since the width of an interval never changes. The number of intervals will go to infinity to get the area under the curve. The limit and the summation are symbolized by the integral from [a,b].

Example:

Find the average value of the given function on the given interval.

f(x) = 1 - 2x [0,3]

Using the average value formula for functions, we can get the average value...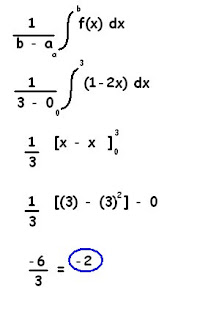

Then, we talked about the Mean Value Theorem for Integrals.

If we recall, the Mean Value Theorem for Derivatives state that: Let f be continuous on a closed interval, [a,b]. There lies a value "c" that is equal to the rate of change of the curve.

The Mean Value Theorem for Integrals state that: Let f be continuous on a closed interval [a,b]. Then there exists "c" in the closed interval such that...

With all that said and done, we practiced 1 problem.

Find the i) average value of "f" on the given interval, ii) "c" such that the average of "f" is equal to the f(c), and iii) sketch the graph of f and a rectangle whose area is the same as the area under "f".

f(x) = 2x [0,3]
I think that's all we did in class. Next scribe is... err.... I'm not sure who to pick. XD I'll just pick during the next class.