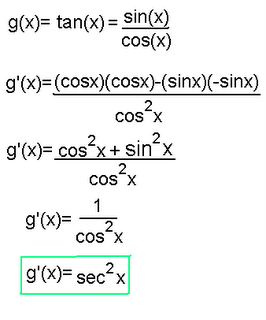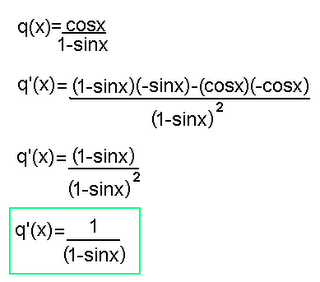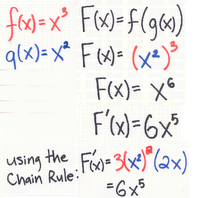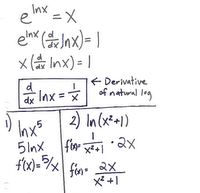Scribe Post - Day 53

So for today's class I chose to volounteer myself to do the scribe in place for Danny, because who would want to do it on their birthday? Not me! So a big happy birthday to Danny!

Anyway back on topic... We started off class with a discussion about our Pedro the Pi-Rate Panda Project, and agreed on certain criteria we are going to follow. Then we were told about the wonderful site Mr.K and Mr.H have put together called studentblogwikitools.wikispaces.com, which has many tools to make a students life much easier online, so click on it and check it out. After we talked about a couple of math contests that offer pretty decent prizes. And lastly we started with the real math.

We began to learn about Newton's Method. Newton's Method is used to approximate the root of any given function.

On the function f(x) = x³ -2x² -5 for example,

-graph-

the function graphically will look sort of like this.

Then you'd pick a value that you suspect is close to the root. In this example we see that the root is somewhere between x=2 to x=3, and closer to x=3. We chose x=2 for our chosen value, and would find the root of its tangent line at that particular point to try to zero in on our zero of the parent function.

-graph-

To do this we must find the derivative of our given function which turns out to
f'(x) = 3x² - 4x.

Just plug in the value 2 in both our derivative and parent function for
f'(2) = 4 and f(2) = -5.

Then we would use our point slope formula to determine any equation for any tangent line at a point which looks like f(x) - f(a) = f'(a)(x-a).
And a is the point we're looking at. And since we're looking for the root of the tangent line, f(x)=0 because roots exists only when the y-value is equal to 0.
Now we would just plug in our values to get 0 - (-5) = 4(x-2) and solve for x.
Which then equals to x = 13/4 which is the root of our tangent line at f'(2).

After we use this new number and repeat the process, finding yet another root of a tangent line at that point, and in this case, the root of the tangent line of where f'(13/4). So we would plug it in again in the same formula which generally looks like - f(a)/f'(a) + a = x after you balance the equation. We would repeat the process until the estimate generally stays the same.

On a calculator it is very simple to do, but you must must must know how to do the Newton's Method by hand, as it will probably show up on the exam. On the calculator though you can do this by first:
- plug in both the parent function and derivative function into Y1 and Y2 respectively
- 2nd quit to the homescreen
- compute in -Y1(2)/Y(2) + 2 and store the value in alpha a
- then 2nd enter for the same equation and press enter again, each time for a better estimate
- noticeably the value should tend to remain the same

And that is Newton's Method, which could pretty much be used for any kind of function, you name it.

However it is very important as to which number you choose to pick first to zero in on the root. It isn't the best method if you do not pick the right number as it could just put you in a circle of incorrect roots like as seen in some of these applications here.

And that comes to a closure of my scribe post. I will definitely spice things up and include graphs for a better picture. But right now I had just came back from my volounteer service, and I'm still in my outside clothes, starving to death without dinner. It's getting late, and I still have other homework to do. Sorry for any inconviences, I will fix it up tomorrow night after work. I have covered pretty much everything though, and if not you can tell me =).

Okay next scribe will be Danny because he said he'll do it =].

Pedro the Pi-Rate Panda Project

Hi! I just want to invite everyone to visit our online project, the link to which should be on the side.

Scribe Post - Day 52

Today Mr. K started off talking about Scribe Posts and told us to check out scribe posts made by students in Scotland. Heres the link:

http://exc-el.org.uk/blogs/s3scribeposts


We then did questions from the text book.

4.7 Exercises - #7

7. f(x)= 1/x at a = 1/2

4.6 Exercises - # 17

17. Two sides of a triangle are equal in length, and each increases at the constant rate of 2 in/min. The angle between these two sides increases at the constant rate of 1 rad/min. Determing the rate of change of the third side at the moment that the other two sides are each 10 inches long and their included angle has a measure of π / 2 radians. [HINT: The Law of cosines may be helpful]

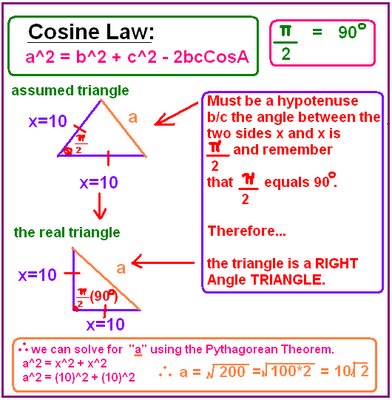
NOTE: I don't think the answer I got is right. I was pretty close though
(da/dt= 14 √2 in/min). I think i did some miscalculations. I was trying to figure out where i went wrong and i still couldn't find the mistake/s . =( Can someone please help me and tell me where i went wrong. That would be greatly appreciated =).....
********Right Answer from back of text: da/dt= 7√2 in/min****************


We then did a group work assignment about Stan the Clause =)


Stan the Clause.

It's Christmas Eve and children are asleep all across the land, waiting for Santa to bring them gifts. However, naughty children will be visited by Stan the Clause in his flying can. Stan is flying over the town in an altitude of 500 feet, heading towards a naughty little boy's house. He is flying at a horizontal speed of 125 mph. Find the rate at which the angle of elevation from the naughty boy's house to the flying can is changing in radians per second when the angle of elevation is
π / 12.

HINT: There are 5280 feet in one mile



























Sorry guys for posting late and if my photos are blurry!!!!!!!!!

I pick u Danny for scribe. : )

SCRIBE POST: DAY 51

Hey guys, I'm your scribe for today. Sorry for the late late post, today was a really bad day for me. Anyway, let's begin! We spent most of today's class solving problems in different groups.

The first one was called BOYS MEETS WEIRD

Borg the turtle was walking across the road (to get to the other side), and a very weird person saw him. Mr. Turtle tried to get away, but alas, he was not so fast. The person subjected Borg to genetic engineering to grow fur on the turtle. Assume Borg is semi-spherical, and the hair grows equally and only on the curved surface. Include hair in the radius and round answers to three decimal places.

1. When the rate of change of the volume is 12 cubic feet per second, and Borg has a radius of 14 ft (he's one huge turtle), what is the rate of change of the radius?

First, we take what we're given and we state what we're looking for.

Then we find a formula that ties the relationship of all the variables we have .

We take the derivative of this formula, and plug in values to solve the problem.

When the rate of change of the volume is 12 cubic feet per second, and Borg has a radius of 14 ft, the rate of change of the radius is .096 ft per second.

2. The weird person wanted Borg to be huggable-soft. This occurs when the rate of change of the volume is 1600 cubic feet/second, and the rate of change of the radius is 13 feet/second. When did Borg reach huggable-soft status (give the radius)?

Again, we take what we're given and state what we're looking for.

We're able to use the same formula from the previous question, and we simply plug in the values to solve the problem.

Borg reaches huggable-soft status at a radius of 13.9 ft.

EPILOGUE: Borg escaped from the weird person and currently lives with a loving rabbit named Thursday =)

The second problem we had was called WILLY'S COVERT OCCUPATION

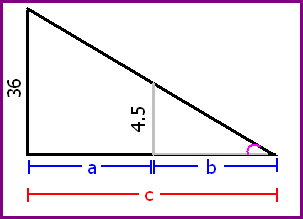Willy the Wallaby is a hard worker, but not devoted enough to work at the circus for almost 70 hours building a tank just so he could be shot out of a cannon like a metal ball. He is convinced there is a better job out there (and he wants to at least keep a shred of dignity). So Willy joins up with his friend Roo and his old coach Spike to seek out a tough guy name Wyman Weasel who has been sending out letter for a covert employment operation offering great pay for the ones with enough "guys and smarts" to find the secret hangout. The instructions began at the ingersection of Crim Dr. and Twotough Blvd. The streetlight on that corner is 36 ft off the ground. The only ones who can get the job have to figure out the rate they have to be moving toward the south end of Crime Dr. in order to have their shadow changing length at a rate of 11/35 ft per second. Once the applicant found the rate, the next instruction was to move at that pace and an escort will approach. The escort will take any animal that moves at the right pace to the clubhouse door. The final password to get in is the rate of change of the tip of the shadow. Willy and his friends want your help to finally get the good paying job they deserve.

Find the rate Willy and his friends must move if they are all 4 ft 6 inches tall, and then find the rate of change of the tip of the shadow.

First, we drew the picture to have an idea of what it looks like and to get a better understanding of the problem.

We can see that there are two triangles in the diagram, and that they are similar. We use this idea to solve the problem.

If 36 is proportional to 4.5, we can use their relationship as a formula. We use the derivative of this relationship to find the rate of change of the tip of the shadow.

From here, we can solve for the rate that Willy and his friends must move by finding another relationship between them and the tip of the shadow. This relationship is obvious in the diagram. Plug in what you have to solve.

The rate of change of the tip of the shadow is 88/35 ft per second, and the rate that Willy and his friends must move is 77/35 ft per second.

We then talked about a square root function and the idea of appoximations.

In this example we are trying to find what the square root of 37 is. We know that the square root of 36 is 6, therefore the answer should be somewhat over that.

We took the square root function and found the derivative of it. Then we plugged in 36 and got the slope.

By writing the equation of a line (remember that a derivative is a slope of a tangent line - we're imaging the straight line between 36 and 37) using the point-slope formula, and plugging in 37, we have an approximation of the square root of 37.

And that my friends brings us to the end of today's class. PHEW! Homework for tonight as I'm sure all of you already know, is EXERCISE 4.7, question 1-9. And just a reminder, we're at the end of the unit soooo you know what that means, get your BOBS up! By the way KATRIN, you're tomorrow's scribe. Goodnight guys =)

Scribe Post

Hello everybody, Crystal here :D

During the beginning of the class we discussed was about our flickr assignment.

http://flickr.com/

--The first part of the assignment was to take a picture of a number. It can be a picture of anything real. Then we post it on flickr and tag it with interesting and apcalc06. We then e-mail Mr. Kuropatwa with the URL of the picture on the flickr site.

--The second part of the assignment is to take a picture of a derivitive, we can set up the picture. Then we post it again on flickr and tag it with derivitive and apcalc06. We're also supposed to describe what a derivitive is, everything that we learned, and also how the picture represents a derivitive. This is due Monday December 4, 2006.

Next we reviewed some of the questions from exercise 4.6 Related Rates. Then we moved on to a group assignment about our hero Scuba Steve!!!

Scuba Steve's Slick Bacteria
While on vacation in Mexico, a tanker accident has spolled oil in the Gulf of Mexico. Scuba Steve volunteered to help by spreading oil-eating bacteria which is gobbling 7 ft²/hr. The oil slick has the form of a circular cylindar. When the radius of the cylindar is 250 ft, the thickness of the slick is 0.02 ft and decreasing at a rate of 0.002 ft/hr.
a) At what rate is the area of the circular top of the slick changing at this time?
b) Is the area of the slick increasing or decreasing?

For this question my group had kind of a slow time starting off. But after awhile we began understanding it after some discussion.

Now we have to differentiate to find the derivitive of the area.

We didn't quite finish this question so if you're group knows how to solve this fully, please help.

Well our homework for today is the rest of exercise 4.6 Related Rates ODD NUMBERS.

Tomorrows scribe is LINGER!!! :D

scribe post

hey guys, its charlene your scribe for today

well as usual we started class with a few problems on the board

1) find Dy/Dx @ (1,1) given

....X^3 + X^4 + Y^3 + Y^2 = 4

....X^3 + X^4 + Y^3 + Y^2 = 4
....
....3X^2 + 4X^3 + 3Y^2 Y^1 + 2YY' = 0

....3Y^2Y' + 2YY' = -3X^2 - 4X^3
....
....Y' (3Y^2 + 2Y ) = -3X^2 - 4X^3

....Y' = -3X^2 - 4X^3
.............3Y^2 + 2Y
...
....Y' = -X^2 (3+4X)
........... Y (3Y + 2)...........---derivative of the function

TO FIGURE OUT THE DERIVATIVE @ (1,1) JUST PLUG IN x=1 AND y=1 INTO THE EQUATION

....Y' (1,1) = -(1)^2 (3 + 4(1))
.....................(1) ( 3(1) +2)

....Y' (1,1) = - 7/5


2) Find the equation of the line tangent to X^2 + Y^3 + 2X^3 + 8Y^2 = 3 @ the point (-1 , 2)


....X^2 3 Y*2 Dy/Dx + 2 X Y^3 + 6X^2 + 16Y Dy/Dx = 0

....Dy/Dx (3X^2 Y^2 + 16Y) = -2XY^3 - 6X^2

....Dy/Dx = -2X ( Y^3 + 3X)
...................Y (3X^2 Y +16)-- <--DERIVATIVE OF FUNCTION

PLUG IN X=-1 AND Y=2 INTO EQUATION

....Dy/Dx (-1 , 2) = -2(-1)(2^3 + 3(-1))
................................2(3(-1)^2 (2) +16)

....Dy/Dx (-1,2) = 5/22

TO GET THE EQUATION OF THE TANGENT YOU USE THE point-slope formula

....POINT = (-1,2)

....SLOPE = 5/22

....Y - 2 = 5/22 (X+1)

3) find the equation of the line tangent X^3 Y^2 = Y +2 @ X=1

...X^3Y^2 = Y+2

....LET X=1

....(1)^3 Y^2 - Y -2 = 0

....(Y-2) (Y+1) = 0

....Y= 2...Y= -1

TO FIGURE OUT THE DERIVATIVE OF THE EQUATION

....X^3Y^2 = Y + 2

....3X^2 Y^2 + X^3 (2Y) DY/Dx = Dy/Dx

....2X^3 Dy/Dx - Dy/Dx = -3X^2 Y^2

....Dy/Dx ( 2X^3Y - 1 ) = -3X^2 Y^2

....Dy/Dx = -3X^2 Y^2
.......................2X^3Y -1

NOW YOU HAVE TO PLUG IN THE POINTS (1,2) AND (1,-1)

....Dy/Dx (1,2) = -3(1)^2 (2)^2
............................2(1)^3 (2)(-1)

........................= -4

....EQUATION Y - 2 = -4 (X-1)

....Dy/Dx (1 -1) = -3(1)^2 (-1)^2
.............................2(1)^3 (-1)(-1)

.........................= 1

....EQUATION Y + 1 = X - 1


AFTER PROBLEMS ON THE BOARD WE LEARNED SOMETHING NEW...

picture a smaller square in the center of a larger square

rate = derivative

sidelength with respect to time

Ds / Dt = 2 cm / sec

between the two sqaures these following things will change

- perimeter

- area -> length of sides depends on time

-diagonal

to calculate the perimeter with respect to time

....Dp / Dt = ?

....P = 4S ** S= LENGTH OF SIDES

....Dp / Dt = 4 Ds / Dt

....Dp / Dt = 4 (2)

....Dp / Dt = 8 CM/S

area with respect to time

....Da / Dt = ?

....AREA = S^2

....Da / Dt = 2 S Ds/Dt

....Da / Dt = 4s

SUPPOSE S = 5CM

....Da/Dt = 4(5)

...............= 20 CM^2 / SEC

Mr. K also showed us a presentation about what we just learned. Mr. K will put a link of the website on the blog.

homework section 4.6, questions 1 - 12

the next scribe is CRYSTAL

Scribe Post

Hello everybody, Mark is your scribe for today.

We started off by looking at this equation:

x²+y²=25
This is not a function, because it is continuous.

x²+(f(x))²
The above equation can be re-written like this, where y is some function of x

(f(x)) is the composite of functions and we can differentiate using the Chain rule.
Since we are finding the derivative, We are finding the derivative with respect to x because we rewrote the function (y) in terms of x.

IN GENERAL:
If you use the chain function to find the derivative of a composite, you find the derivative of f with respect to u. Which looks like this

F(x)=f(u(x))

Original Notation
F'(x)= f'(u(x)) x u'(x)

*new notation*
Leibniz Notation
F'(x) = df/du x u'(x)
= df/du x du/dx
= df/dx

Finding the implicit definition of x² + y² = 25

2x + 2yy' = 0

2yy '= -2x

y' = -2x/2y

y' = -x/y
This is the most common way of seeing the Leibniz notation. The x value will be given so all you have to do is plug it in, but to find the y value, we must go back to the original equation to find the y value.

The steps used in the above implicit differentiation requires to think abstract. We must remember y is a composite of functions. Also when a function is given, to write the implicit definition we assume the function can be written in terms of x.

NOTE: When finding the values of y on a function, use the difference of squares. The difference of squares will show the negative and positive values.

Here are questions that we for the last half of the class.

1) find dy/dx @ x=10, for x-2y=4

x - 2y = 4

1 - 2y' = 0

-2y' = -1

y' = 1/2

2)find dy/dx @ x=12, for x - 2y² = 4

1 - 4y'= 0

1 = 4y'

1/4y' = y' y Dependant

so we go back to original equation and solve for y

12 - 2y² = 4

8 = 2y² = 4

4 = y²

y² - 4 = 0

y= 4, -4

@ (12. 2) y' = 1/8

@ (12,-2) y' = -1/8



3)4x² + 9y² = 36
find (1, 4/3 x square root of 2)

8x + 18yy' = 0

9yy' = -4x

y' = -4x/9y


y' (1, 4/3 x square root of 2) = -4(1) / 9(3 x square root of 2)

= -4/(12 x square root of 2)

= -1/(3 x square root of 2)

4)12x² - 3y² = 48

24x - 6yy' = 0

yy' = -4x

y' = -4x/y


12x² = 48

x² = 4

x² - 9 =0

x = 2, -2

























Hw: 4.5 all odds, flickr pics, tag as apcalc06 and interesting. See post below

CharLENE is our next scribe.

It's All In Your Hands

This picture shows that 7 x 7 = 49 ... click on it to find out how. ;-)

Don't forget about your flickr assignment.

Cheers!
Mr. K.

Scribe Post

Hey guys, it's Lindsay again. We started class with the usual white board questions. For some of the questions we used the
CHAIN RULE:
F(x) = f(g(x))
F'(x) = f'(g(x))g'(x)

1. Differentiate.




































2. f(x) xe^-3x
a) find f'












b) find f"











c) determine the interval(s) where f is increasing
(-infinity, 1/3)
d) determine the interval(s) where f is concave up
(2/3, infinity)

3. Given the equation below, solve for y and differentiate
x² + y² = 25






IMPLICIT means that it's SUGGESTED without having it IN YOUR FACE!
A circle isn't a function but we can still find the derivative for it by looking at one section of it.


The next scribe is MARK

Scribe Post

Hi guys this is Suzanne :)

Today we started off with the following questions:

1)Find the x-coordinates where f '(x)= 0 of the following:

First of all we find the derivative by using the Quotient Rule, and then use a calculator to find the root. Note that the denominator can never equal zero so you just need to find the roots of the numerator. If you input the whole thing into your calculator it will not work.

2. Differentiate:

a)

b) The derivative here can be found by using the Quotient rule, by using sin and cos to describe tan.

c) This derivative is found using the product rule.

d) This question once again uses the Quotient rule.

After those questions we were given f(x) and g(x) and asked to find F(x) and F '(x). Using paint takes way too long so i just wrote these, just ignore how horrible it looks. I'm sure there was a much easier way to do this, but I can't think of one right now.

Anyway, using the chain rule seen below, we can find the derivative of composite functions. The order in which the functions are composed DOES matter. f(g(x)) is not the same as g(f(x)).

And this last awful diagram tells us that the derivative of a natural log is 1/x. The 1st example shows that you have to apply logarithmic rules before using the derivative rule.

And that's about it.. sorry this isn't great but I'm kind of technology impaired it seems. Next scribe is.. Mark. Though I'm a bit confused.. are we just starting a new cycle? Or has the scribe list not been updated in a bit? Anyway, I'll hope for the best.

scribe

Hey it's Anh...I'd like to start things off by apologizing for missing this scribe post which should have been done but didn't...I can't really excuse what did not get done but I honestly did not know that I was scribe which is no excuse at all but hey it's the truth. Anyways to correct that mistake here it goes...

Note: The information in the blue box is basically giving you the derivative of each of those functions. The work below this box just proves the statements in the box.

This feels like a short scribe post but I can't remember what we did on Friday...were we talking about the rubric? Maybe that was a different day god...this is why you should never procrastinate well in this case always keep up to date with things...like checking out the blog.

Sorry Suzanne for the short notice for scribe =/..thank you very much

Anyways...I hope this scribe post lives up to the standards and someone out there hopefully learns something from it.

.............................................................................

.............................................................................

.............................................................................

Excellence and habit--

Do you think??

Scribe Post: Day 44

Hi guys! This is Jann and I'll be your scribe for today.

Again, we started with 2 questions. Here we go...

1. On what intervals is the function, f(x) = x^4 - 4x^3 + 10, both concave down and decreasing?

Solution:

First, we have to find the first and second derivatives of the given function.

Note: Remember, the first derivative determines the graph of f if its increasing or decreasing. The second derivative determines the concavity of the parent function, f. By simplifying the first and second derivatives, we can determine the roots of each equation.

Using these roots, we can use the number line test to find which interval is the graph of "f" concave down and decreasing by substituting values on each interval.

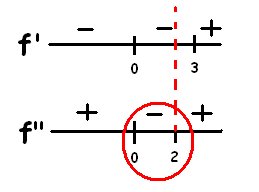
Since the interval (0,2) agrees on both number lines, we can say that on the interval (0,2), the graph of the parent function is both concave down and decreasing.

2. "f" has a domain [-5,5]. The second derivative is shown below.

a) On what interval(s) is "f" concave up?

Solution:

On the interval (-4,1), the graph of the 2nd derivative is above the x-axis. Since the graph of f" is positive, it means that the graph of the first derivative is increasing. Therefore, the graph of the parent function on the interval (-4,1) is concave up.

b) Where does "f" have any points of inflection?

Solution:

The roots of the 2nd derivative are x = -4,1. On these points, the graph of the first derivative have either a local min or max. If there is a local min or max, then the parent function must be shifting from either positive to negative or negative to positive.

c) Suppose that f'(1) = 0. Is "f" increasing or decreasing at x=4? Explain.

Solution:

The parent function is decreasing at x = 4 because the graph of the 2nd derivative starts to decrease at x = 1. If the graph of the 2nd derivative is below the x-axis, then the graph of the first derivative must be negative. If the graph of the first derivative is decreasing, then the parent function must be decreasing. The graph of the 2nd derivative is also shifting from positive to negative.

The face example...

Mr. K asked, "Can you tell if I'm standing on top of a mountain cliff or on a valley with my face zoomed in the picture??" No, because we're only focusing on his face. We can't tell where he is because we don't pay attention to the surroundings. We can apply this concept on the previous problem. In part (c), could we answer the question if we focus our attention on x=1? If we look around the graph, we could make a better and more accurate conclusion to answer the question.

Lastly, we talked about 2 new rules: Reciprocal and Quotient Derivative Rules

Mr. K told us something to help us remember the quotient rule. LO DI HI MINUS HI DI LO ALL OVER LO LO [key words: HI-f(x) LO-g(x) DI HI(LO)- f'(x)/g'(x)]

I guess thats about it. Whew, I almost went crazy cuz blogger suddenly went offline on me. I had to start things over again. T.T Anyways, I hope I mentioned everything we did today. Next scribe will be.... uhh... ANH!

The Product Rule

Today we found the Product Rule for derivatives and as usual we had white board questions!

1. f(x) = x³ + 2x² - 8x + 1
Find the equation of the tangent line at x=2

f(2) = 1

f'(x) = 3x² + 4x - 8
f'(2) = 3(2)² + 4(2) - 8
= 3(4) + 8 - 8
= 12 + 8 - 8
= 12

equation: y - 1 = 12(x-2)

2. g(x) = x^3/2 - x^1/2
Find the equation of the tangent line x=4

g(4) = 6

g'(x) = (3/2)x - (1/2)x
g'(4) = (3/2)x^1/2 - (1/2)^-1\2
= (3/2)(4)^1/2 - (1/2)^-1\2
= 11/4

equation: y - 6 = 11/4(x-4)

3. Multiply
(x + 3)(2x +5)

I know that everyone can easily do this problem but this is going to help us derive the product derivative rule. I wasn't taught how to multiply by using "the area model of multiplication" and it probably wouldn't have changed how i multiplied but it will serve its purpose in the next question. Mr.K showed us an example with (x + 3)(2x +5)

= 2x² + 11x + 15

With this example, it helped me understand how to find the derivative rule of F(x)=f(x) g(x).

The first thing we had to do was find the areas of I, II, and III

Area I: [g(x+h) - g(x)]f(x)

Area II: [f(x+h)-f(x)]g(x)

Area III: [f(x+h)-f(x)][g(x+h)-g(x)]

With these areas, we were able to derive the product rule of the derivative.

The Product Rule of the Derivative is f(x)g'(x) + g(x)f'(x).

No Homework today. My work here is done. Jann, I choose you!

Trying harder, reviewing more OR being more effective?

Greetings AP Calculus! From your BOBs, it appears you are really working hard and feeling that to be more successful, you need to "keep trying", "review more", and "figure it out". My sense is you are really doing that now; I wonder if you think you could be more effective in your efforts? I know from lots of experience (60 years worth) that habits can ensure my reaching my goals or not. And often, I've tried harder, and reviewed more, but not really effectively. Given that, I think I've found 7 habits, that if I've worked at them, have helped me be more effective! Have you seen these 3? Do you think these habits can be of value to you too? Or are these a habit for you already?

--------------------------------------------

I think this short autobiography is a good introduction to Habit 1.

There's A Hole In My Sidewalk: AUTOBIOGRAPHY IN FIVE SHORT CHAPTERS

by Portia Nelson
Chapter 1
I walk down the street.
There is a deep hole in the sidewalk.
I fall in.
I am lost.... I am hopeless.
It isn't my fault.
It takes forever to find a way out.
Chapter 2
I walk down the same street.
There is a deep hole in the sidewalk.
I pretend I don't see it.
I fall in again.
I can't believe I am in the same place.
But, it isn't my fault.
It still takes a long time to get out.
Chapter 3
I walk down the same street.
There is a deep hole in the sidewalk.
I see it is there.
I still fall in.... It's a habit.
My eyes are open.
I know where I am.
It is my fault.
I get out immediately.
Chapter 4
I walk down the same street.
There is a deep hole in the sidewalk.
I walk around it.
Chapter 5
I walk down another street.

Habit 1: Be Proactive®
Take responsibility for your life.

--------------------------------------------------------------

Does this cartoon say it all for Habit 2?

Habit 2: Begin with the end in mind.®
Define your mission and goals in life..

-----------------------------------------

Finally, Habit 3: Rocks, Pebbles, Sand, Water—And Calculus is which?

A time management specialist was asked to give a presentation on her specialty. She decided to do a demonstration. First she asked her assistants to bring a big bucket and put it on the table in front of the audience. Then she asked for large, grapefruit-sized rocks and filled the bucket with them.
"Is the bucket full," she asked?
"Yes!" said the crowd, but she asked for more to put in anyway. This time her assistants brought in pebbles. She poured the pebbles in the bucket and it held a surprising number in the space between the big rocks.
"Now is the bucket full?" she asked.
"Yes!" "No!" "Yes!" "No!" said various persons in the crowd. Some people were uncertain; some were getting suspicious. The time management specialist asked for more. This time the assistants brought her sand. She poured sand in the bucket and it filled the spaces between the pebbles.
"Now is the bucket full?" she asked.
"No!" they answered. By now, everyone was suspicious. So she asked for water and poured in quite a lot. Now no one could think of anything else that could fit in that bucket.
"What does this process demonstrate?" asked the time management specialist.
One member of the audience spoke up: "No matter how busy you are, you can always fit in one more thing."
"I can see how you might think that was my point, but it is not," said the specialist. "I was trying to show you that if you don't put the big rocks in first, you'll never get them in at all!"

Habit 3: Put First Things First®
Prioritize and do the most important things first.

What do you think?
Best,
Lani

And by the way, these come from 7 Habits of Highly Effective Teens by Sean Covey.

Scribe Post: Day 42

Today we learned the derivative rule for an exponential function.


f(x) = a ^x
f(x+h) = a ^x+h

f ' (x) = lim f(x+h) - f(x) /h
h->0

= lim a ^x+h + a ^x /h
h->0


When you graph the parent function and its derivative on your calculator you'll find that the graphs are very similar. The y-intercept of the functions is different. This must mean that there a constant, C, to multiply with that varies the y-intercept.

f ' (x) = C a^x


In the table of values, the values of both of the graphs are doubling. In Y3, if you put y2/y1, you will find the constant value. When x = 0, the output is the same.

Try different values of a, and find the constant value , C.

* this is supposed to be my table, sorry if it looks kind of weird *

A C f(x)

2 0.693 f ' (x) = o.693 (2 ^x)
3 1.098 f ' (x) = 1.098 (3 ^x)
e 1.000 f ' (x) = 1 (e ^x) * this is a special number *
4 1.386 ...
5 1.610 ...
6 1.791 you can see the pattern here, so I don't want to type all these eq'ns =)
7 1.941 ...
8 2.077 ...
9 2.197 ...

We are finding the derivative of the parent function at x=0, and that gives us the constant.

_________________________________________________________


f(x) = e ^x
f' (x) = e^x
e ^x is a special number because it is its own derivative.

_________________________________________________________

Now back to the table. If you plot this on your calculator, the graph looks similar to a square root function, but if you use the stat key on your calculator you can find the accuracy it fits on the graph. A second that fits much much better it the natural log , Lnx.

From this fact, we have found that Ln x is the constant of the derivative at!
eg.
ln2 = 0.693
lne = 1

___________________________________________________

f '(x) = lim a ^x+h + a ^x / h
h->0

= lim a^xa^h - a ^x/ h
h->0
* we used the law of exponents above*

= lim a ^x ( a^h-1 ) / h
h->0
* a ^x was factored out *

= a ^x * lim (a^h-1 ) / h
h->0
* a ^x was taken out of the limit b/c it will not be affected by h*

f ' (x) = a ^x * lim (a^h-1 ) / h
. h->0

lim (a^h-1 ) / h is the derivative of the parent function at x = 0.
h->0
_______________________________

p ^x has a slope of 1 at x = 0.

lim p ^x - p ⁰ / (x-0)
x->0

p ^x - p ⁰ / x = 1

p ^x - p ⁰ = x

p ^x = x + p ⁰

p ^x1/x = (x+1)^1/x

p = (x+1)^1/x * graph this on your calculator *

As x -> 0 it approaches e.

e = lim (x+1)^1/x

Homework for tonight is 4.2, odd questions. Due for wednesday, I don't if that means to hand in =( ... does it? Anyway, the next scribe is Lindsay.


hehe I thought this was funny...

thats
. like
. my brain
after


. math


sometimes.

BOB

Integrals was actually a pretty short unit which is cool. It wasn't too hard of a unit to understand and there wasn't anything too puzzling about it. At first I was a bit confused with the different ways on a calculator you can find an integral like the program "RSUM". Often I would forget to put the function into my Y1 value and I'd come up with this whacky answer from the program =P Then the whole left:, right:, x choice:, and number was a little confusing to me at first until Suzanne and Christian helped me out with it, thanks guys =D I'm hoping I can do ok on this test, this is the first test I'm going to have in this course where I feel comfortable going into haha!

bob

integrals are interesting...haha...well I think I understand integrals well enough but then again sometimes when I think I really understand something I don't..anyway I think I understand the concept of finding the area under the curve. The thing that's got me a little "bamboozled" is when they give a function and ask to evaluate it...I just don't understand what to do and I tried looking it up in the solution book..you know what I think I'll go check again and try to figure it out. Anyways off to study the "definite integral".

Scribe Post: Day 41

NOTE that all the derivative rules are in bold and red. All the calculations are in bold. All explanations are in normal text. I will state the rule first, then go through the steps that show how to get it.

.

DERIVATIVE RULES

.

There are many ways to solve derivatives. Just in our class, we learned about 8-9 ways. In this unit, we are going to find the rules that help us solve for derivatives super easily. We are going to find the derivative rules for Linear Functions (y = mx + b), Constant Functions (y = c), Functions with Constant Variables ( kf(x) ), Exponential Functions (xⁿ), and sum and difference functions (-+).

.

Definition of a derivative:

.

f'(x) = lim_h-->0 [f(x+h) - f(x)]/h

.

In order to find the derivative rule, we must:

(1) Take the general equation for the function, and

(2) substitute in (x+h) wherever there's an x.

(3) We plug in what we get from step 2 to "f(x+h)" on the definition of a derivative.

(4) We reduce the terms we get as much as possible to get the rule.

.

Linear Functions

.

f'(x) = m

.

f(x) = mx + b

f(x+h) = m(x+h) + b

.

f'(x) = [m(x+h) + b] - mx + b

= (mx + mh + b - mx + b)

= mh/h

= m

.

Constant Functions

.

f'(x) = 0

.

f(x) = c

f(x+h) = c

.

f'(x) = lim_h-->0 (c - c)/h

= lim_h-->0 0

.

Functions with Constant Variables

.

f'(x) = kf'(x)

.

F(x) = kf(x)

F(x+h) = kf(x+h)

.

F'(x) = lim_h-->0 F(x+h) - F(x)/h

= lim_h-->0 kf(x+h) - kf(x)/h

= lim_h-->0 k[f(x+h) - f(x)]/h

= lim_h-->0 klim_h-->0 f(x+h) - f(x)/h

= k lim_h-->0 f(x+h) - f(x)/h

We know that this is the definition for a derivative, so wherever you find this, you can just subsitute f'(x)

= kf'(x)

.

This rule is important, because when a function has a constant, we can just mulitply the derivative by the constant.

.

This is all for now. I still have to do the rules for polynomial functions (e.g. x³, x⁴ etc.) and sum and difference functions, but it's soooo hard to do on the computer. Sorry for the inconvencience guys; I tried. There's lots of fractions over fractions, fractions to polynomial exponents and so forth. It just gets really confusing. So I'll just neatly write them on paper and scan it. I'll edit this post later on, so just check it out.

.

The next scribe is Ashlynn. I can't pick Madame President, Lindsay, because both of us, including katrin and linger won't be in Tuesday's class. Someone else pick her =).

.

.

.

(Please ignore the dots =). I just put them cause when I publish or save, my whole post gets compressed; all the spaces are gone. So to make things clearer, I added these thingies. Sorry)