SCRIBE POST: DAY 51

Hey guys, I'm your scribe for today. Sorry for the late late post, today was a really bad day for me. Anyway, let's begin! We spent most of today's class solving problems in different groups.

The first one was called BOYS MEETS WEIRD

Borg the turtle was walking across the road (to get to the other side), and a very weird person saw him. Mr. Turtle tried to get away, but alas, he was not so fast. The person subjected Borg to genetic engineering to grow fur on the turtle. Assume Borg is semi-spherical, and the hair grows equally and only on the curved surface. Include hair in the radius and round answers to three decimal places.

1. When the rate of change of the volume is 12 cubic feet per second, and Borg has a radius of 14 ft (he's one huge turtle), what is the rate of change of the radius?

First, we take what we're given and we state what we're looking for.

Then we find a formula that ties the relationship of all the variables we have .

We take the derivative of this formula, and plug in values to solve the problem.

When the rate of change of the volume is 12 cubic feet per second, and Borg has a radius of 14 ft, the rate of change of the radius is .096 ft per second.

2. The weird person wanted Borg to be huggable-soft. This occurs when the rate of change of the volume is 1600 cubic feet/second, and the rate of change of the radius is 13 feet/second. When did Borg reach huggable-soft status (give the radius)?

Again, we take what we're given and state what we're looking for.

We're able to use the same formula from the previous question, and we simply plug in the values to solve the problem.

Borg reaches huggable-soft status at a radius of 13.9 ft.

EPILOGUE: Borg escaped from the weird person and currently lives with a loving rabbit named Thursday =)

The second problem we had was called WILLY'S COVERT OCCUPATION

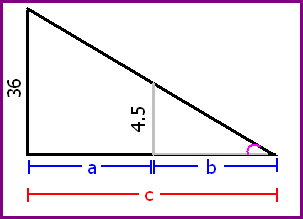Willy the Wallaby is a hard worker, but not devoted enough to work at the circus for almost 70 hours building a tank just so he could be shot out of a cannon like a metal ball. He is convinced there is a better job out there (and he wants to at least keep a shred of dignity). So Willy joins up with his friend Roo and his old coach Spike to seek out a tough guy name Wyman Weasel who has been sending out letter for a covert employment operation offering great pay for the ones with enough "guys and smarts" to find the secret hangout. The instructions began at the ingersection of Crim Dr. and Twotough Blvd. The streetlight on that corner is 36 ft off the ground. The only ones who can get the job have to figure out the rate they have to be moving toward the south end of Crime Dr. in order to have their shadow changing length at a rate of 11/35 ft per second. Once the applicant found the rate, the next instruction was to move at that pace and an escort will approach. The escort will take any animal that moves at the right pace to the clubhouse door. The final password to get in is the rate of change of the tip of the shadow. Willy and his friends want your help to finally get the good paying job they deserve.

Find the rate Willy and his friends must move if they are all 4 ft 6 inches tall, and then find the rate of change of the tip of the shadow.

First, we drew the picture to have an idea of what it looks like and to get a better understanding of the problem.

We can see that there are two triangles in the diagram, and that they are similar. We use this idea to solve the problem.

If 36 is proportional to 4.5, we can use their relationship as a formula. We use the derivative of this relationship to find the rate of change of the tip of the shadow.

From here, we can solve for the rate that Willy and his friends must move by finding another relationship between them and the tip of the shadow. This relationship is obvious in the diagram. Plug in what you have to solve.

The rate of change of the tip of the shadow is 88/35 ft per second, and the rate that Willy and his friends must move is 77/35 ft per second.

We then talked about a square root function and the idea of appoximations.

In this example we are trying to find what the square root of 37 is. We know that the square root of 36 is 6, therefore the answer should be somewhat over that.

We took the square root function and found the derivative of it. Then we plugged in 36 and got the slope.

By writing the equation of a line (remember that a derivative is a slope of a tangent line - we're imaging the straight line between 36 and 37) using the point-slope formula, and plugging in 37, we have an approximation of the square root of 37.

And that my friends brings us to the end of today's class. PHEW! Homework for tonight as I'm sure all of you already know, is EXERCISE 4.7, question 1-9. And just a reminder, we're at the end of the unit soooo you know what that means, get your BOBS up! By the way KATRIN, you're tomorrow's scribe. Goodnight guys =)