EXPLORATORY WORKSHEET: (PG.179)
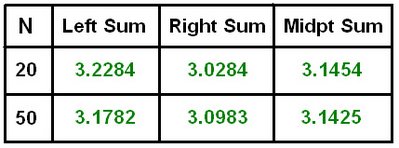
Use the RSUM program to calculate the lefthand (C= 0), righthand (C=1) and the midpoint (c=0.5) approximating sums for each of the following definite integrals. Use 20 and 50 equally spaced subdivisions.
1)

Some Tips:
On T1-83 Calculator:
*****DON'T FORGET TO STORE FUNCTION GIVEN IN [Y=]*****
- To get RSum, go [PRGM] -> RSUM (NOTE: to get RSUM PRGM go see pg.168)
- On the home screen, it should say prgmRSUM, press [ENTER]
- Left: 0 [ENTER] bottem subcript (left # in interval)
- Right: 2 [ENTER] upper supcript (right # in interval)
- X CHOICE: either ---> C=O (LEFT SUM) / C=1 (RIGHT SUM) / C=0.5 (MIDPT SUM) [ENTER]
- NUMBER: either ---> N=20 / N= 50 [ENTER]
- Press [ENTER]
- YOU GET SUM=_________
.
2)
*****DON'T FORGET TO STORE FUNCTION GIVEN IN [Y=]*****
- To get RSum, go [PRGM] -> RSUM (NOTE: to get RSUM PRGM go see pg.168)
- On the home screen, it should say prgmRSUM, press [ENTER]
- Left: 1 [ENTER] bottem subcript (left # in interval)
- Right: 2 [ENTER] upper supcript (right # in interval)
- X CHOICE: either ---> C=O (LEFT SUM) / C=1 (RIGHT SUM) / C=0.5 (MIDPT SUM) [ENTER]
- NUMBER: either ---> N=20 / N= 50 [ENTER]
- Press [ENTER]
- YOU GET SUM=_________
.
Some Tips:
On T1-83 Calculator:
*****DON'T FORGET TO STORE FUNCTION GIVEN IN [Y=]*****
- To get RSum, go [PRGM] -> RSUM (NOTE: to get RSUM PRGM go see pg.168)
- On the home screen, it should say prgmRSUM, press [ENTER]
- Left: 0 [ENTER] bottem subcript (left # in interval)
- Right:1 [ENTER] upper supcript (right # in interval)
- X CHOICE: either ---> C=O (LEFT SUM) / C=1 (RIGHT SUM) / C=0.5 (MIDPT SUM) [ENTER]
- NUMBER: either ---> N=20 / N= 50 [ENTER]
- Press [ENTER]
- YOU GET SUM=_________
4)Which of the two methods, midpouint or endpoint Riemann sums, seem to give better approximations to the definite integral? Try to give a general explanation for your conclusion.
.
Midpoint Riemann sums seems to give better approximations to the definite integral because it decreases the amount of error, thus making the integral more approximate. Scientifically, when we increased the number of subintervals to N=50, the amount of error decreased, thus approximating a definite integral.
.
..
5) Use the fnint (command on your T1-83 to obtain another approximation of each integral above. Comment on the degree to which the estimates of the definite integral agree.
The degree to which the estimates of the definte integral agree, but by using the fnInt (command on your T1-83), it obtains a more approximate integral. The definte integral approximation is correct to nine digits, using the command on your T1-83 -> fnInt.
HOMEWORK: SUPPLEMENTARY PROBLEMS odd #'s
The next scribe person will be...MANNY. =)
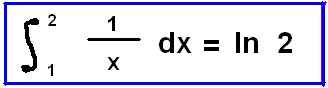




No comments:
Post a Comment