Scribe Post: Day 44

Hi guys! This is Jann and I'll be your scribe for today.

Again, we started with 2 questions. Here we go...

1. On what intervals is the function, f(x) = x^4 - 4x^3 + 10, both concave down and decreasing?

Solution:

First, we have to find the first and second derivatives of the given function.

Note: Remember, the first derivative determines the graph of f if its increasing or decreasing. The second derivative determines the concavity of the parent function, f. By simplifying the first and second derivatives, we can determine the roots of each equation.

Using these roots, we can use the number line test to find which interval is the graph of "f" concave down and decreasing by substituting values on each interval.

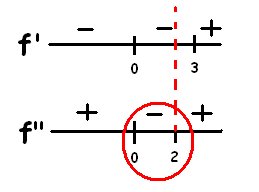
Since the interval (0,2) agrees on both number lines, we can say that on the interval (0,2), the graph of the parent function is both concave down and decreasing.

2. "f" has a domain [-5,5]. The second derivative is shown below.

a) On what interval(s) is "f" concave up?

Solution:

On the interval (-4,1), the graph of the 2nd derivative is above the x-axis. Since the graph of f" is positive, it means that the graph of the first derivative is increasing. Therefore, the graph of the parent function on the interval (-4,1) is concave up.

b) Where does "f" have any points of inflection?

Solution:

The roots of the 2nd derivative are x = -4,1. On these points, the graph of the first derivative have either a local min or max. If there is a local min or max, then the parent function must be shifting from either positive to negative or negative to positive.

c) Suppose that f'(1) = 0. Is "f" increasing or decreasing at x=4? Explain.

Solution:

The parent function is decreasing at x = 4 because the graph of the 2nd derivative starts to decrease at x = 1. If the graph of the 2nd derivative is below the x-axis, then the graph of the first derivative must be negative. If the graph of the first derivative is decreasing, then the parent function must be decreasing. The graph of the 2nd derivative is also shifting from positive to negative.

The face example...

Mr. K asked, "Can you tell if I'm standing on top of a mountain cliff or on a valley with my face zoomed in the picture??" No, because we're only focusing on his face. We can't tell where he is because we don't pay attention to the surroundings. We can apply this concept on the previous problem. In part (c), could we answer the question if we focus our attention on x=1? If we look around the graph, we could make a better and more accurate conclusion to answer the question.

Lastly, we talked about 2 new rules: Reciprocal and Quotient Derivative Rules

Mr. K told us something to help us remember the quotient rule. LO DI HI MINUS HI DI LO ALL OVER LO LO [key words: HI-f(x) LO-g(x) DI HI(LO)- f'(x)/g'(x)]

I guess thats about it. Whew, I almost went crazy cuz blogger suddenly went offline on me. I had to start things over again. T.T Anyways, I hope I mentioned everything we did today. Next scribe will be.... uhh... ANH!