Hey kids, it's Loso and I was today's class scribe. Today we were given three questions to do, to follow up on what we learned yesterday [technically speaking, it's what you all learned yesterday because I wasn't in class yesterday, SORRY!].
QUESTIONS:
1. Dave invests $100 at 8% interest per year. How much does Dave have after 6 years if the interest is compounded;
a) annually
b) quarterly
c) continuously
2. The population of New Hampshire was 1 million in 1990. It doubles every 25 years. What is it today?
3. Describe all the features and properties of the graphs of:
a) y-2
xb) y=3
-xSOLUTIONS:
1. a) Since we're given a sufficient amount of information, we can use the A=
P(1+
r/
n)
tn formula. I'm pretty sure you all know how to plug in the information, but just for every one's sake, let's make sure.
A is what we're looking for.
Our
principle amount is
$100 [
P].
1 is taking 100% of what we already have and then adding it with the rate of interest.
Our
rate of interest is
8%, and is
0.08 when written as a decimal [
r].
6 is the
amount of time we're looking at. [
t]
n is the
number of times we compound a year. In this case, we're compounding
once every year.
A=P(1+r/n)
tnA=100[1+(0.08/1)]
(6)(1)A=100(1.08)
6We were able to leave it at that for today.b) We use the same formula, with the exception that we're compounding
4 times a year, instead of once a year.
A=P(1+r/n)
tnA=100[1+(0.08/4)]
(6)(4)A=100(1.02)
24c)For c, we use A=Pe
rtA=Pe
rtA=100e
(0.08)(6)A=100e
(0.48)2. For this question, we use A=Ao(M)
t/pA=Ao(M)
t/pA=1,000,000(2)
15/25Umm, I kind of missed the answer. He was going through it pretty quickly. Hopefully I did that right.3.

These are what the graphs look like.
y=2x
-increasing function (or grows exponentially)
-asymptote is y=0
-DOMAIN (-∞, ∞)
-RANGE (0, ∞)
-y int. y=1
-no roots
-concaves up
y=3-x
-decreasing function (or exponential decay)
-asymptote is y=0
-DOMAIN (-∞, ∞)
-RANGE (0, ∞)
-y int. y=1
-no roots
-concaves up
Everything in purple is what is similar between both functions.
We then discussed how to describe what an inverse was.
VERBALLY: An inverse of a function is a function that undoes what the parent function does. You can also say, the inputs become outputs, and the outputs become inputs
He brought up the baby play and parent clean up example. I think we're all pretty clear of what the point of that was.
NUMERICALLY: This was the example we were given, basically showing how the y values become x values, and the x values become y values.

GRAPHICALLY:

Yeah, I know the lines look wrong, but it's the best I can do right now so bear with me. Near the end of the class, there was some discussion about one to one functions, which at this time is quite vague to me. It's late and my brain needs rest. Our homework is exercise 1.6, all odd questions including 10,18,28 and 30.
For the next scribe, I choose Suzanne. Have fun with that. =)
 Hi guys! This is Jann(again) and I'll be your scribe for today. (^_^)
Hi guys! This is Jann(again) and I'll be your scribe for today. (^_^)

 Double Angle Identities:
Double Angle Identities: The properties are:
The properties are: Note: The standard form for a sine function is f(x)= AsinB(x-C)+D; where A=amplitude, B= Period, C= face shift, D= vertical shift.
Note: The standard form for a sine function is f(x)= AsinB(x-C)+D; where A=amplitude, B= Period, C= face shift, D= vertical shift. The class came up with these 2 formulas:
The class came up with these 2 formulas: Here are the steps to graph this table:
Here are the steps to graph this table:

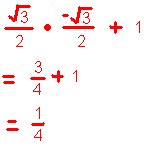



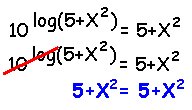

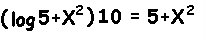

 The graph of this function is invertible because it passed the horizontal line test.
The graph of this function is invertible because it passed the horizontal line test. 
 a) This function had two roots, but when you graph it on your calculator, it appears at first glance to have three roots. There are several ways to determine whether or not there is a root.
a) This function had two roots, but when you graph it on your calculator, it appears at first glance to have three roots. There are several ways to determine whether or not there is a root. Method 3: Finally, we can find the
Method 3: Finally, we can find the 





