In class, we found out that our blog will be visited by many countries and that’s just fantastic I think. Since there will be a lot of people visiting, we have to follow some guidelines. Please read the “Students Made This” entry. It’s for homework, so I suggest reading it. =)
It’s like second nature to start class with questions on the whiteboard. I don’t entirely understand everything we talked about this class so please comment to explain things better. =) please and thank you.
A function, f, is given by the formula
f(x)=R/(x+k)
Where R and K are constants. If the points A(3,2) and B(5,1) both lie on the graph of f, determine the numbers R and k exactly.
Solution:
f(x)=R/x+k ; k cannot = -3
2=R/3+k
f(x)=R/x+k ; k cannot = -5
1= R/5+k
6 + 2k = R
6 + 2k = 5 + k
1 = -k
k = -1
6 +2 (-1) =R
R = 4
2. Without using your calculator sketch each pair of functions on the same graph.
a) f(x)=x^2
g(x)=x^2-4

general rule: f(x)+ k
the graph shifts up when k is postive and shifts down when k is negative.
b) f(x)= √ (x)
g(x)= √(x-2)
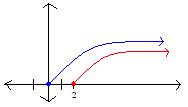
general rule: f(x+k)
the graph shifts to the right when k is negative and shifts to the left when k is postive.
c) f(x)=sinx
g(x)=-2sinx
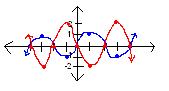
general rule: kf(x)
if k > 0, it will stretch vertically
if 1 > k > 0, graph will compress by a factor of k
in this function, there is a vertical stretch by a factor of 2. since it's -2, it reflects over the x axis.
d) f(x)= √(4-x^2)
g(x) = √(4-(2x)^2)
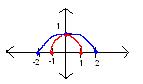
general rule: f(kx)
if k > 1, the function will compress horizontally.
if k HOMEWORK: 1.2 odd numbers and question 16.
I choose Crystal to be the next scribe. =)
Be happy,
Lindsay.

7 comments:
LINDSAY; I think you did a good job on your scribe. I know it's hard to explain the general rule for those functions, but if you read the textbook it will really help... it talks about basic functions and shifting, stretching, compressing and gives examples as well. I think after reading that we'll all have a better understanding of the general rules for the functions we had on the board.
Lindsay, this was great as a first scribe! I liked the way you used colour in a meaningful way and the graphics you included went a long way towards helping understand what you were writing.
A couple of things you might like to edit:
#2 (a) The parabola was not stretched, it was shifted -- down in the example. The general rule you give below is for stretches [kf(x)]. The general rule for vertical shifts is: f(x) + k.
The graph shifts up when k is positive nad down when k is negative.
#2 (b) and (d) You gave the correct general rule, but didn't describe it.
When you use this symbol: √ for roots, if you also use brackets carefully it is easier to follow your work ...
compare:
√x^2 - 4
to
√(x^2 - 4)
All in all a scribe well done. With a few minor edits you can kick it up another notch! ;-)
I'm VERY frustrated right now.
FIRST: I was commenting on lindsay's post when my laptop overheated and turned off. USELESS COMPUTER! Unfortunately I can't recall most of the things I said there, but I'll do my best.
SECOND: I was re-doing my comment when I accidentally deleted my re-do comment. I copied it a bit earlier for back-up BUT I copied over it with Mr. K's root sign. SO I'm doing this again. Just not a computer day for me.
THIRD: I was in one of those rare days when I actually wanted to do math. However, I left my textbook in Mr. K's room. Apologies sir, I'll make up to it somehow.
OKAY!
Lindsay, I think your work was excellent. You touched on the things we discussed in class, and it really helped me.
Please correct me if I'm wrong with my addition.
The graphs of
f(x) = √(4 - x^2) and
g(x) = √(4 - (2x)^2)
are in Lindsay's post. If we notice, the only values that changed between the first and second equation is that in the second, "x" became "2x". Before the function does its work (as Manny put it I think), the input is first doubled. The effects are counter-intuitive because the larger the input is, the less the output becomes. For example:
In f(x) = √(4 - x) where x is 0, the output is 2.
if x = 2, however, the function would look like
f(x) = √(4 - 2), then
f(x) = √(2)
f(x) = approximately 1.4
IT'S SMALLER!! There you go.
Lindsay's wise words:
Be happy,
Christian
Hey Lindsay,
Your scrib is very well explained. I like the way you graphed the functions. I agree with Mr. K's correction regarding the brackets with the sq roots. Anyways, good job with the scrib!
Hey Lindsay,
Your scrib is very well explained. I like the way you graphed the functions. I agree with Mr. K's correction regarding the brackets with the sq roots. Anyways, good job with the scrib!
=) i like your graphics lindsay... those graph drawings take long lol.
Christian, that's hilarious. i actually forgot my book in my locker lol.
Post a Comment