Today we started off with the following questions:
1)Find the x-coordinates where f '(x)= 0 of the following:
First of all we find the derivative by using the Quotient Rule, and then use a calculator to find the root. Note that the denominator can never equal zero so you just need to find the roots of the numerator. If you input the whole thing into your calculator it will not work.
2. Differentiate:
a)
b) The derivative here can be found by using the Quotient rule, by using sin and cos to describe tan.
c) This derivative is found using the product rule.
d) This question once again uses the Quotient rule.
After those questions we were given f(x) and g(x) and asked to find F(x) and F '(x). Using paint takes way too long so i just wrote these, just ignore how horrible it looks. I'm sure there was a much easier way to do this, but I can't think of one right now.
Anyway, using the chain rule seen below, we can find the derivative of composite functions. The order in which the functions are composed DOES matter. f(g(x)) is not the same as g(f(x)).
And this last awful diagram tells us that the derivative of a natural log is 1/x. The 1st example shows that you have to apply logarithmic rules before using the derivative rule.
And that's about it.. sorry this isn't great but I'm kind of technology impaired it seems. Next scribe is.. Mark. Though I'm a bit confused.. are we just starting a new cycle? Or has the scribe list not been updated in a bit? Anyway, I'll hope for the best.
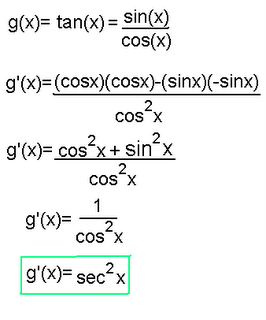
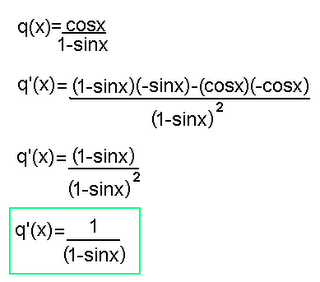
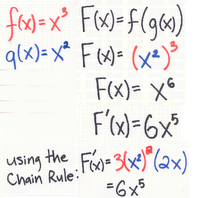
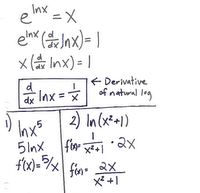
No comments:
Post a Comment