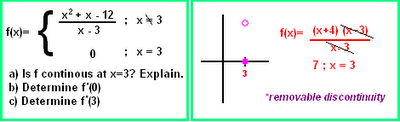
Well, I was completely surprised to find out that I was scribe for today. This being due to the fact that my internet was being evil this weekend, and I didn't realize we were already on round 3 of the scribe (this year's passing by so fast!) So this post is brought to you by Linger, who informed me of my duty (thanks again!)
Today we got started on chapter 3. This is the problem we looked at in class:
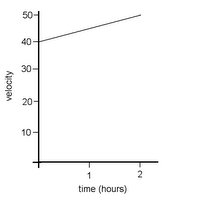
Manny is driving through the USA to Fargo. Between noon and 2pm his speed increases steadily from 40mph to 5mph.
1)Draw a graph of his speed over time.
2)Estimate his minimum distance travelled.
3)Estimate his maximum distance travelled.
1)
2) d=vt 3) d=vt
=(40)(2) =(50)(2)
=80 miles =100 miles
So, how did we get the answers for questions 2 and 3?
First, we are looking for the minimum possible distance travelled over the entire 2 hour period. We know that he was travelling at
at least 40 mph throughout the entire trip. So by using the formula
d=vt, (which most people probably know from physics) we get our answer. We know that there is no way that Manny could have travelled less than
80 miles. But because we know that he travelled at more than 40 mph as the trip went on, we know that 80 miles is an
underestimate.
The same applies to question 3. We know that Manny was
never travelling more than 50 mph throughout the trip. So he can't possibly have travelled more than
100 miles in that time. And because we know that it was only at the end that he reached a speed of 50mph, we know that 100 miles is an
overestimate.
So now we know that the distance travelled over 2 hours is somewhere
between 80 and 100 miles. We can also look at the solution to these questions from a graphical perspective.
2) 3)
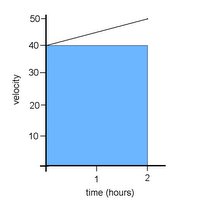
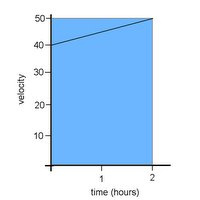
In grade 10 science most of us learned that we could
find distance on a velocity-time graph by finding the area underneath the line. This is exactly what we did to solve for questions 2 and 3, except that now we are no longer dealing with nice, happy horizontal lines. So the minimum and maximum possible values we found earlier don't show us the exact distance travelled, because we are not considering the rate of change in our answers. Instead, we're saying:
If the velocity had been 40mph over the entire trip then the distance would be 80 miles. If the velocity had been 50mph over the entire trip then the distance would be 100 miles.This only gives us a rough estimate of the actual distance travelled. The area is either
underestimated or overestimated, our margin of error is shown by the white triangle under the first graph, and the blue one over the second graph.
So, the next step is: how do we make our answer more accurate? What if we use the same method as before, but look at each hour seperately? We get these graphs:
2) 3)
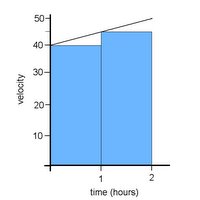
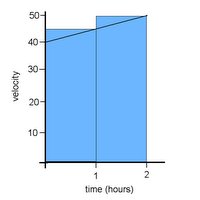
And by calculating the total shaded areas and adding them together, we find:
2) d1= (40)(1) d2= (45)(1) 3) d1= (45)(1) d2= (50)(1)
total d= 85 miles total d= 95 miles
Before we knew that the total distance travelled was
between 80 and 100 miles.
Now we know that the total distance travelled is
between 85 and 95 miles.
So we have narrowed down our error by half, from
20 miles to just
10.
We can also see the margin of error decreasing from the graphical perspective, as we see the triangles showing
underestimation or overestimation are decreasing in area.
And if I were to feel up to making even more graphs, with more lovely blue rectangles, an even more accurate answer could be found.
Now, imaginate that we have an infinite number of little blue rectangles on our graph. The margin of error approaches zero, and we have an accurate answer, which makes us very happy :) In other words, we're just finding the exact area underneath the line.
Now, for a bit of technical stuff. How do we know if we are underestimating or overestimating?
When the graph is increasing, like the one in our example today:
If we take the areas using velocities starting from the left, the answer will be an underestimate.
If we take the areas using velocities starting from the right, the answer will be an overestimate.
When the graph is decreasing:
If we take the areas using velocities starting from the left, the answer will be an overestimate.
If we take the areas using velocities starting from the right, the answer will be an underestimate.
And the new term of the day is
Monotonic. This means that the function is always increasing or always decreasing. Tomorrow's scribe is Linger. Happy Haloween tomorrow, everyone. And I can't get this to look quite the way I want, so I'm sorry if there are weird unecessary spaces or the numbers get squashed. I don't know how to fix it.
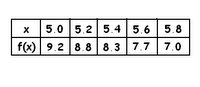
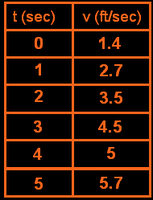 The velocity of an object, in feet per second, is given in the table.
The velocity of an object, in feet per second, is given in the table.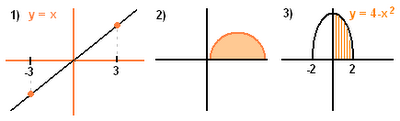 Area is width multiplied by the height. Integral is the signed area under a curve. If you look at the first example, from 0 to 3 the area you would get is 9/2. You would also get the same area from -3 to 0. But if we're talking about integrals, the integral from 0 to 3 is 9/2 and the integral from -3 to 0 is -9/2.
Area is width multiplied by the height. Integral is the signed area under a curve. If you look at the first example, from 0 to 3 the area you would get is 9/2. You would also get the same area from -3 to 0. But if we're talking about integrals, the integral from 0 to 3 is 9/2 and the integral from -3 to 0 is -9/2.