The derivative function

Class started off with completing some questions off of the board...

1) Suppose f(x)=√(x)

calculate the average the rate of change between:

a) x=9.0 and x=9.1

b) x= 8.9 and x=9.0

c) Use your answers to a) and b) to approximate the instantaneous rate of change at x=9.

Solution:

1)a) (3.0166-3.0)/(9.1-9.0)= 0.166

b) (3.0-2.9833)/(9.0-8.9)= 0.167

c) (0.166+0.167)/2= 0.1665

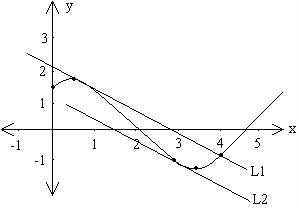
2)a) On the given of f sketch a line whose slope is (f(4)-f(1)/4-1) label the line L1.

b) Now sketch a line whose slope is lim h->0 (f(3+h)-f(1)/h) label the line L2.

* lim h->0, refers to the fact that h gets closer to zero but never gets there.

3) If g(x)=│x^4-16│, what can you say about the values:

a) g'(4)

b) g'(2)

c) g'(0)

Solution:

a) postive number, derivative is 256.

b) derivitive should not exist although the calculator gives you an answer you must discard it because the calculator is stupid.
c) horizontal line, slope is zero.

*derivative- to find the slope of tangent line.

Mr.K then handed out a worksheet on The Derivative Function which is to be done for homework.

Here are the questions from the worksheet...

Investigation 1

Consider the function f(x)= x^2-2. Using your calculator, graph the function. Using the [DRAW]:[Tangent] feature, calculate the slope of the tangent line for x= -3, -2, -1, 0, 1, 2, 3.

Consider the relationship between x(the values in the first row) and the slope of the tangent (the values in the third row). Find a function (f '(x)) that relates the tow rows in the table. Use your calculator to graph both functions.

Investigation 2

Consider the graph below. Estimate the slope (the derivitive) of f for all integral values of x illustrated. Plot these new ordered pairs (f ') on top of the given graph.

Investigation 3

Consider the table of values below. Use the data in the table and the difference quotient to estimate the value of f '(x) for each given value of x. Complete the table of values for f '(x).

Use the statistical graphing feature of your calculator to plot both table of values as broken line graphs.

Investigation 4

The derivative of a function f(x) can be defined as the limiting value of the difference quotient as h approaches 0: f '=lim(h->0) ( f(x+h)-f(x) )/h. Use this definition to determine the derivative of f(x)=1/x algebraically. Use your calculator to graph both functions.

Tomorrow's scribe is Katrin =)