Scribe Post

Hey guys, sorry for the big delay on my scribe post. I was having some technical difficulties with my computer, my notes and with some of the calculator work, so please accept my apology. On the up side, to compensate for the delay on my scribe post, I was actually on time for class for once. It shouldn't have to be a rarity but, I'm trying.

Alright, so to start our class, we picked up on our derivatives unit and started off with a couple of problems given to us on the board.

QUESTIONS

1. A ball is dropped from a height of 400ft and falls towards the earth in a straight line. In t seconds, the ball falls a distance d(t) = 16t² feet.

a)How long does it take the ball to hit the ground?
b)What is the average velocity of the ball during the time it is falling?
c)Estimate the instantaneous velocity of the ball when it hits the ground.

2. An object travels in such a way so that its position at various points in time are given in the table:



a) Find the average velocity of the object between t = 1.3 and t = 1.9.
b) Estimate the instantaneous velocity at t = 1.9.

SOLUTIONS

1. Keep in mind, this problem is similar to the one we were working on the day before, with Charlotte's driving trip to Gimli.

a) To figure out how long it takes for the ball to hit the ground, we know that it'll hit the ground at 400 ft, so we simply take 400 ft and plug it into our given equation to find the time it takes.

d(t) = 16t²
400 = 16t² [plug in 400 as our output]
25 = t² [divide both sides by 16]
5 = t [square root each side]

Hence, our answer is that it takes 5 seconds for the ball to hit the ground.

b) We take the rate of change formula and take the two values that we already know. We know that when x is 0, y is 0, and when x is 5, y is 400.

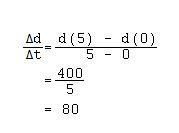
c) We can estimate that the instantaneous velocity is 160.

2. a) Again, we use the rate of change formula to figure out the average velocity.



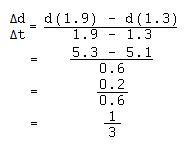
b) We can estimate that the instantaneous velocity at t = 1.9 is -2.


Then, we talked about secant lines and tangent lines. Given the graph to the left as an example, we want a tangent line at point c. If we take various points of the function and connect it to point c with secant lines, we are getting infanantly close.

If you take a fixed point, and a point on a curve and create a secant line that moves infinitely close, we create a tangent line.

The slope of the tangent line gives us the instantaneous rate of change. We created a way for us to find the tangent line of any value by programming our calculators.



We were given an example to plug into our y₁ coordinates, which when plugged in gave us a curve [sorry, but I didn't write down the example down right]. We wanted to get closer to one, so we zoom in a number of times until the curve started to look like a straight line.

To get our little program going we press [prgm] and selcet NEW at the top. We want to call it SLOPE. At the top of your screen, it should say PROGRAM : SLOPE. Press enter and you should be on a new line with a coland automatically beginning it. You have to input these "instructions" for the calculator, hitting enter to start each new line:

:[TRACE]
:X[STO]A
:Y₁[STO]B
:[TRACE]
:X[STO]C
:Y₁[STO]D
(D-B) / (C-A) [STO] S
:Disp "SLOPE", S


Trace is the blue button underneath your screen.
Hitting store on the calculator will display an arrow on your screen.
We uses the alpha key to punch in the letters.
To get th "Disp" command, we hit [prgm], use the right arrow button and arrow to "I/O"(it stands for inputs/outputs) and Disp should be the 3rd choice down.

When we were done we just 2nd quit and were done with creating the slope. We then used our example and used the slope program created to find the tangent line at -1.

Our homework that was assigned to us was section 2.2, all odd questions including questions 2, 4 and 10. I picked Anh to be the next scribe.