Before going over what we did today, I just want to remind everyone about the test tomorrow. I hope everyone will do great! XD Anyways, here we go:
In the beginning of class, we went over the last 2 questions in the pre-test.
(5) Suppose a function "f" is defined so that it has derivatives:

Over what interval is the graph of "f" both increasing and concave up?
Solution:
To identify what interval is "f" increasing and concave up, first find the roots of the two equations:
f'(x)= x^2(x-1)= (x^2+2)(x-1), x= 0,1
f"(x)= x(3x-2)= (x+0)(3x-2), x= 0,2/3
Then, use the number line method for each equation.
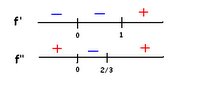
We can see that at the intervals x>1 and x>2/3, the answer is positive. Therefore, the graph is increasing due to f' and concave up due to f" since both are positive.
The answer is x>1. The number 1 is not included because the graph increases after x=1.
(6) Consider the following table of data for the function "f".
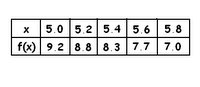
(a) Estimate f'(5.2) as acurately as possible.
Solution:
In order to estimate f'(5.2), we use the Symmetric Difference Quotient method. Since the given is a table of values, we can get the slope to the left and to the right of x= 5.2 Then, we get the average of the 2 slopes.

(b) Write the equation for the tangent line at x= 5.2
Solution:
To get the equation of the tangent line at x= 5.2, we could use the point-slope formula using the pt (5.2,8.8) and the answer to 6a.
y-y1= m(x-x1)
y-8.8= -9/4(x-5.2)
(c) Use your answer to part b to find approximately, f(5.26)
Solution:
Using the formula found in part b, we could simply substitute f(5.26) as "y" and 5.56 as "x".
y-8.8= -9/4(x-5.2)
f(5.26)-8.8= -9/4(5.26-5.2)
(d) What is the sign of f"(5.2)? Explain your answer.
Solution:
f"(5.2) is "negative" because the first derivative of the parent function is decreasing due to the slopes -2 and -2.25 Because the slopes are decreasing, the 2nd derivative at these points are negative.
After going over the last 2 questions, we were given another group problem. Here's the function of the problem.

I forgot how the questions were typed, so here are the answers anyways. XD
Solution: The graph of the function

The graph is constantly increasing from negative infinity up to x=3. As soon as it reaches x>3, the graph jumps up in a parabolic funcion. Therefore the graph is discontinuous and nonremovable. Its not a good idea to but grain from this company because if you buy more than 3 bags at $9, the next bags would be higher that the rate of the first 3 bags.
Finally, we were given 2 problems.
1)

a) Is "f" continuous at x=3? NO
b) Determine f'(0)= 1
c) Determine f'(3)= does not exist
2)
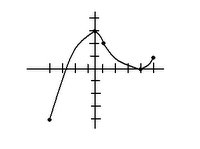
a) On what interval is the graph of "f" concave down? (-3,-2)
b) Where on the graph of "f" will there be a point of inflection? x=-2
c) If "f" is decreasing at x= -2.5, is "f" increasing or decreasing at x=-2.Explain Decreasing
Tip of the Day: Enter nDeriv(Y1,X,X) in your Y0 and leave it there until we throw away our calculator, I guess. =P If you put this on your calc, you dont have to re-enter this command in Y2 every time you need to find the derivative of the function in Y1.
I think thats all we did today. Sorry if my post is colorless(besides blue and black). I dont know why, but the tool bar on top is pretty... short? The color and font size menus are missing. 0.0 Anyways, good luck to ya'll tomorrow!! =D
Oh yah I almost forgot. Next Scribe for Monday is... Suzanne!

No comments:
Post a Comment