Scribe Post Day 30

Today was basically a review of the Derivative Function.

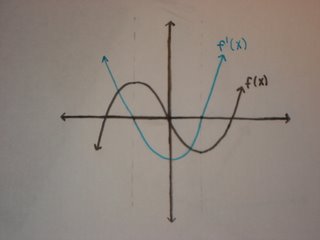
The derivative function is the slope of the tangent lines of the parent function. When there is a zero, or root, of the derivative function, f'(x), we know that there will be a maximum or a minimum. This means that tangent lines are horizontal, with a slope of zero, on the parent function.

The blue graph is the derivative of the parent function.

F'(x) has two roots where x= -a, and x=a.

At x= -a, the graph of F '(x) is going from positive to negative, meaning that the parent function has a maximum at x= -a. The slopes of the tangent line on the parent function change from positive to negative after x = -a.

At x= a, F '(x) is going from negative to positive, meaning the the slopes of the tangent lines of the parent function at x = -a, are going from negative to positive. From that we know the parent function has a maximum at x = a.

___________________________________________________________________

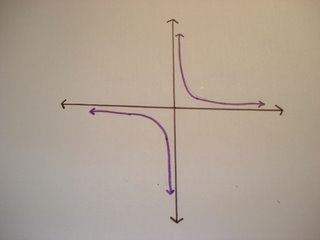
The derivative function for this graph exists for everywhere on the graph of F(x) except at x = 0. At x = 0, there is a root but the derivative is undefined. This is because if you find the slope to the left and right of 0, you would end up with different slopes where one would be negative and the other is positive. At x = 0, there is a corner, making it impossible to find the derivative. It is not locally linear because no matter how much we zoom in on the graph there will always be a corner.

____________________________________________________________________

There are a number of ways to find the slope of a graph;

1) Use the slope program on your calculator.

2) Use your calculator to draw the tangent line at a point.

3) Use "nderive( " on your calculator.

Your calculator uses the difference quotient to find the slopes of the tangent lines. Your calculator also tries to use this at a point where the derivative should be undefined. If it gives a slope at that point then your calculator is lying.

4) You can use dy/dx, but before you use this you need the graph of the function on your calculator.

5) lim f(a+h) - f(a) / h

h->0

6) lim f(x+h) - F(x) / h You can use this to find the derivative function

h ->0

ex) f(x) = x ²

f(x+h) - F(x) / h = [ (x+h) ² - x² ] / h

=[ x² + 2xh +h² - x² ] / h

lim 2x +h

h->0

F '(x) = 2x

___________________________________________________________________

The blue graph, F(x), is the parent function.

The pink graph, F '(x), is the derivative function.

F '(x) is undefined at x = 0, it is negative to the left of 0. This means that the parent function has negative slopes for the tangent lines to the left of x = 0.

To the right of x = 0, F '(x) is positive. It must mean that the parent function has positive tangent lines to teh right of x=0

This is the second derivative, F "(x), of the derivative of the parent function, as seen above.

On F "(x), the graph is negative. This means that the parent function is concave down.

When F "(x) is positive, the parent function is concave up.

The point of inflection is at x = 0 or undefined on F "(x), because F '(x) is undefined at x = 0.

__________________________________________________________________

Continuity - a function is continuous if you can draw a graph without lifting your pencil.

A function is continuous if

I lim F(x) exists

x -> a

II F(a) exists

III lim F(x) = F(a)

Mr. K also said to look up the word stymieing .

stymieing - (1)a situation or problem presenting such difficulties as to

discourage or defeat any attempt to deal with or resolve it. (2) to hinder, block, or thwart.

Homework for tonight was to finish up the summary exercise. Tomorrow's scribe will be ... Charlene