SCRIBE POST DAY 29: REVIEW OF CHAPTER 2

Heey guys, it is Linger here once again at your service =) Like always, we had these questions on the board...

1. FIND THESE LIMITS:


Limits can be solved algebraically and technically (calculator). To solve limits algebraically, all you have to do is manipulate what you're given until you have an answer. *careful now... because numbers such as zero and two over zero are possible answers. When we get answers like zero over zero or infinity over infinity, we can use three different techniques to solve the limit...

• factor and reduce
• complex fractions
• radicals and rationalizing

When solving for limits technically, for example in d) we simply plug in the function on our Y= screen, graph it and look for the hole, or look at our table of values and determine where both sides of the function are approaching a certain value. In this case, the limit is 0. NOTE: TO TAKE AXES OFF, GO TO 2ND ZOOM, AND PICK AXES OFF. You should be able to see that there is a whole in the graph at zero, in your ZOOM 4 WINDOW.

2. GRAPH OF g:

Keep in mind that in order for the limit to exist, the right and left hand of the function have to be approaching the same place.

CONTINUITY Graphically, a function is continuous if you are able to draw the graph without lifting your pencil... this is ALWAYS true for all absolute value functions and many other functions. Formally, a function is continous on an interval [a,b] if for all x=a:

• I.....f(a) exists
• II ...lim...f(a) exists
• .....x->a
• III ..f(a) =.. lim....f(x)
  ..................x->a

We learned that the three types of discontinuity are removable, jump, and infinite. An example of an infinite discontinuity is the function of f(x) = 1 / (x-2 ). We also talked about the INTERMEDIATE VALUE THEOREM.

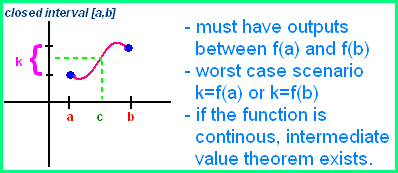
The EXTREME VALUE THEOREM also known as the EXISTENCE THEOREM :

In a closed interval, somewhere between a and b, an output bigger than all the others and an output smaller than all the others have to exist, in order for the function to be continuous.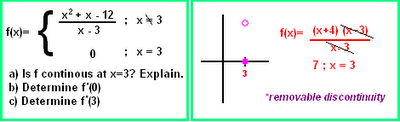

3. A FUNCTION IS GIVEN BY;


* We didn't go over this question in depth, but on the right is what I got down. Basically, we factored the numerator and simplified. We used direct substitution and found that it is a removable discontinuity.

That brings us to the end of today's lesson. FOR HMWK; CHAPTER 2 SUPPLEMENTARY PROBLEMS ODD NUMBERS ONLY. We WILL be having our pre-test and test by the end of this week... STUDY HARD =D And Ashlynn, I CHOOSE YOU !!!!