"Functional" Detectives / Day 26

Well first off to all you skippers that missed class today, no homework! So rest assured =). Anyway, in today's class we started off by being split into two groups and was handed an assignment that we had only 5 minutes to do. Don't worry it wasn't for marks.

Wocertine Eats Like a Cow!

The amount of grass that Wocertine the cow consumes over a period of time increases at a decreasing rate and modeled by G(t), where G(t) equals the amount of grass consumed, and t equals time in hours since Wocertine started eating.

If lim Δx->0 [log((9+Δx) + 1) - 1] / Δx represents the deivative of G(t) at a certain point a

1) Find G(t)
By looking at the equation of the derivative function of G(t), it is noticeable that, that it is the same as the slope formula we've been running into all course. It can be interpreted as lim h->0 [f(a+h) - f(a)] / h.
But in this function in the problem a is a certain point. But we want to know what the function of G(t) would look like. So just replace the "a" for "t."
Therefore G(t) = log(t+1)

2) Find a
Well since G(t)=log(t+1) and a is one point on the graph. And the function f(a)=1 in this equation. So log(a+1)=1 has to be true. And so concludes that a = 9


Then we went on to a problem on the whiteboard.

Graph of f '


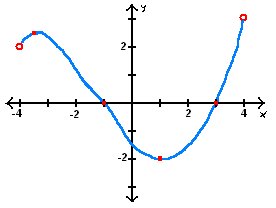
a) Where is f increasing? decreasing?
From looking at the derivative graph of f', we can see where f increases and decreases. Here's a rule of thumb.. where ever f' is above the x-axis, f is increasing and where ever f' is below the x-axis, f is decreasing. Therefore...
increase at (-4,-1) or (3,4)
decrease at (-1,3)

b) Where is f concave up? concave down?
The second derivative graph f'' will tell you if it is concave up or down with the same rule as the derivative. To find f'', find the derivative of f'. So where ever f' has positive slopes, f is concave up, and when it's negative, it is concave down. Therefore...
concave up (-4,-3) or (1,4)
concave down (-3,1)

c) If f(1)=0 is f(0) positive or negative? Explain
Because at f(1)=0, the graph is on the x-axis, but on the derivitive function it shows f is decreasing. Therefore f(0) is positive because it is a point before it decreases into the x-axis where f(1)=0.
f is positive.

We did this type of problem before, but now it's easier to do. Practice makes perfect! And as to whether or not you would use round or square brackets... always use the round brackets in this class when dealing with derivatives. However you will not get marked wrong either way, but just to be on the safe side.

Sometime in class today we also talked about the most famous contributers or creaters maybe of Calculus. We talked about Archimedes, Leibenite, and Newton. Google search these guys if you want to learn about what they did.

And that's a wrap. I'm sorry if I wasn't clear or anything, or caused confusion. It's been quite a day today. And I'll conclude things off by naming the next scribe. And Danny it's you, just because. Good stuff!