Scibe Post: Day 25

Fig. 1

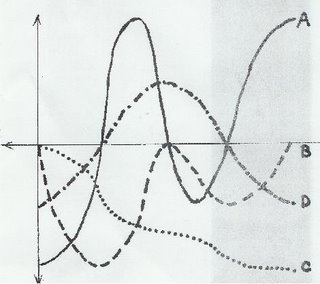
Fig. 2

Hi it’s Christian! In today’s class, we started off with another problem solving sheet like we did on Friday. Given a series of curves (Fig. 1), we were to determine the (1) parent function (2) derivative function (3) second derivative function (4) unrelated. We had about 12.5 minutes to solve the problem and submit the paper. The results are as follows:

a) Parent function is C
b) Derivative function is B
c) Second derivative function is A
d) D is unrelated

Knowing these answers are not enough. More importantly, we should be able to explain our answers. It would show that we understand the question if we can put in plain words how we got the answer right?

We went over the explanations for this problem with Mr. K, and without a doubt he can more eloquently state the solutions. Here, however, is a group of students’ take on the problem. Hopefully this would give you ideas on how to deal with questions such as this.

Here it goes:

Taking a first glance at the graphs was… WOOW! All these squiggly lines throwing us off and making us confused. At first we didn’t know where to start. Honestly, we just blurted out what we know from Friday’s class about graphs, picked one of the curves and tried to find what could be its derivative.

I think my group picked B, and found that its derivative is A. After this, however, we didn’t know what to do anymore. One member said that we should discard C, because it looks weird and not fitting to the rest. Another group member suggested, though, that it shouldn’t be discarded.

The slope of C is, this person noticed, always negative. It would mean that if this has a derivative function, it would exist, for the whole interval, below the x-axis. Lo and behold, there was one curve that was always below the x-axis – B! Now that’s not enough to prove anything. So, we took a more scientific look at this problem and tackled it as such. We looked at the graphs in different parts (Fig. 2).

The derivative function is the slopes of all tangent lines of a parent function. We solved our answers with this fact. Other things such as the candidate local extrema (explained later) of a function, known by the roots of its derivative function, concavities and inflection points, were all used to verify what we came up with, not to solve it. It would be confusing to look at so many factors, given a limited time. So, as I said, we divided the illustration where the roots are (just so that it’s easier to keep track of them), checked the slopes at these intervals and see where they match and where they don’t. Simple as that!

SOLUTION:

We first thought that the parent function is C, as explained above. It’s decreasing throughout the interval, so the derivative function has to be below the x-axis. B fits this criterion and not anything else. Notice that where C seemingly plateaus, B touches the x-axis. This, again, is fitting because where C is horizontal, its slope should be zero. That’s what happens on B. This makes B the derivative of C.

This is where taking the graph into parts becomes important. We are now to find the derivative function of B. We are just validating our assumptions right now, and then discarding those that don’t make sense later.

In part I, B is decreasing, hence f”(x) should be below the x-axis here.

In part II, B is increasing, hence f”(x) should be above the x-axis.

Part III, B is decreasing, hence f”(x) should be below the x-axis. A is below the x-axis in this part, but not D. This is an important clue, but let’s move on before we make further conclusions.

Part IV, B is increasing, hence f”(x) should be above the x-axis. A, again, fits, but not D. If we can prove that D is not the derivative function of anything, and is not the parent function, then we can discard it.

The slope of D is positive in the beginning, and midway through becomes negative. This would mean that its derivative function must start above the x-axis, then, where D’s slope changes from positive to negative, goes below the x-axis. None of the other graphs fit this, therefore it cannot be f’(x). It is also not the parent function, since it has no derivative function. For this problem, then, D is unrelated.

If B is the derivative function of C, and A is the derivative function of B, then C must be f(x), B must be f'(x) and A must be f"(x). We were right! That's all about the problem.

We proceed on to the Relationships between the Parent Function, First Derivative Function, and Second Derivative Function.

A derivative function, f'(x), is the slopes of all tangent lines on the parent function. The value of f'(x)'s roots is zero (0). This means that the tangent line on f(x) where f'(x) = 0, is horizontal. This also proposes candidates for local extrema. Local extrema simply means local minima and/or local maxima. When we have a root on the derivative function, we know the tangent line is horizontal on f(x). We don't know, however, if it is a local maximum or local minimum. That's why we say "candidates for local extremes".

Note:

There aren't always derivatives on the parent function. We are smarter than average bears, and our calculators are stupid. Given a graph, we should know whether there could be a tangent line or not. For corners or cusps, the calculator will say there ARE horizontal tangent lines where the local extrema are, giving us a value of zero. We know that's NOT true. Cusps and corners turn "immediately". If you take the limit of a secant line (two points, one fixed, one moving closer and closer to the other), you'll have something undefined. TAKE A NOTE OF THIS!

Concavities. The concavity of the parent function say something about the second derivative function, f"(x). In an interval where f(x) is concave up, f"(x) exists above the x-axis. Where f(x) is concave down, f"(x) is below the x-axis. The roots of the second derivative function indicate the points of inflection on the parent function, which are the specific places where f(x) changes concavity.

OKAY HERE'S THE DEAL. The first derivative test and second derivative test are mentioned, not concretely, somewhere in this post. The first to tell us what they are, and what they're for will receive candy and a hugg from me (the hugg is optional)! I want people to actually look for details in my post, and for it to be interactive. COMMENTS MUCH APPRECIATED!

Tommorrow's class is the ever competent, ever-holy-cow-smart MANNY! I chose Manny because we (several people) won't be in tomorrow's class, so we need someone we can trust, and someone who would make a "super" post. Yes, that's you dude!