first we were put into groups and we had to work on a worksheet regarding problem solving with derivitives, after that we went through the answers. we then had a question on the board also dealing with derivitives. finally we discussed as a class on how to draw a derivitive function, and we also talked about the first derivitive test.
heres the problem solving worksheet we got...
Willy the Wallaby
Willy the Wallaby and his friends decided to race each other one afternoon. Willy, being the super-powered marsupial that he is, volunteered race first, His position is described by the function f(t). Roo, his friend from school, raced against him, and his position is represented by g(t), the line tangent to f(t) at t=0. They started at t=0 and raced for 8 seconds. Whoever ran the furthest at the end of 8 seconds was the winner. Who won the race and why?
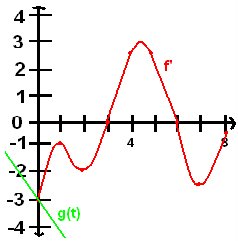
The winner of the race is ROO. Roo wins the race because he ran the furthest in 8 seconds.
-Roo runs in a straight line in a negative direction at a constant speed of -3 (slope of tangent at t=0. while Willy changed direction at t=3 and t=6. Willy's veocity is not constant, because Willy changes direction twice he slows down and even comes to a complete stop for a moment. Due to Willy changing direction twice Roo ran the further distance.
Problem on the board...
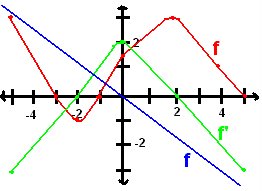
questions
a) where is f' positive? negative?
b) where is f'' positve? negative?
c) what are the critical numbers of f?
answers
b) where is f'' positve? negative?
c) what are the critical numbers of f?
answers
a) positive (-2,2) , negative (-5,2) u (2,5)
b) positive (-5,0) , negative (0,5)
c) critical numbers (roots from parent function) = 2 , 3
We also discussed a little about the first test on derivatives. Heres some stuff on the first test...
1) if the derivative is negative on the left side of the critical point (root) and positive on the right side, then the critcal point is a minimum
2) if the derivative is positive on the left side of the critical point and negative on the right, then the critical point is a maximum
3) if its any other case than it is not a minumum or a maximum
NO NEW HOMEWORK ASSIGNED.
carry on from thursday's homework...
MR PRESIDENT, CHRISTIAN
is the scribe....
b) positive (-5,0) , negative (0,5)
c) critical numbers (roots from parent function) = 2 , 3
We also discussed a little about the first test on derivatives. Heres some stuff on the first test...
1) if the derivative is negative on the left side of the critical point (root) and positive on the right side, then the critcal point is a minimum
2) if the derivative is positive on the left side of the critical point and negative on the right, then the critical point is a maximum
3) if its any other case than it is not a minumum or a maximum
NO NEW HOMEWORK ASSIGNED.
carry on from thursday's homework...
MR PRESIDENT, CHRISTIAN
is the scribe....

No comments:
Post a Comment